7.4. Формулы Максвелла-Мора для определения перемещений в стержневой системе

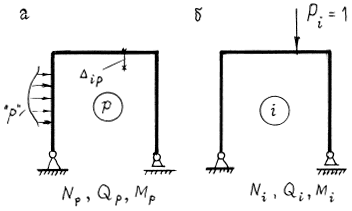
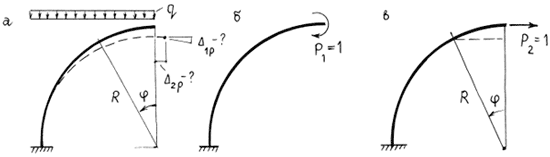
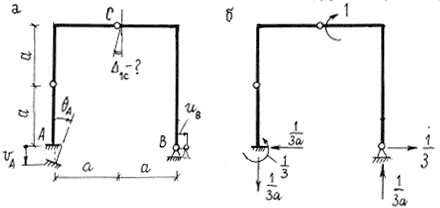
Внешнее воздействие – силовое. Рассмотрим некоторую стержневую систему, например, изображенную на рис. 7.7,а, под действием произвольной внешней нагрузки "p". Требуется определить одно из перемещений системы, вызванное этой нагрузкой, например, . Состояние стержневой системы под действием внешней нагрузки обозначим p , и в нем возникают внутренние усилия .

Ту же стержневую систему рассмотрим под действием единичной силы , соответствующей (по месту и направлению) искомому перемещению. В этом, i - ом, состоянии в стержневой системе возникают внутренние усилия .

Работа, совершаемая внешними силами i-го состояния (это сила и вызванные ею опорные реакции) на перемещениях, вызванных силами в состоянии p,

Далее воспользуемся формулой (7.5), заменив индекс k на p :

(7.7)

(7.7) -формула Максвелла-Мора для определения перемещений от силового внешнего воздействия. Замена текущей координаты x на L подчеркивает то, что ось стержня может иметь любое направление, быть прямолинейной и криволинейной.

Итак, для определения любого перемещения в стержневой системе от внешнего силового воздействия следует рассмотреть два ее состояния: одно (вспомогательное) – под действием единичной силы, соответствующей по месту и направлению искомому перемещению, и другое (основное или "грузовое") - под действием заданной нагрузки. В обоих состояниях необходимо определить распределение внутренних усилий. Подбор нужной единичной силы упрощается с помощью табл.1.

Таблица 7.1

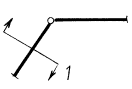
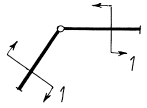
Искомое обобщенное перемещение	Единичная обобщенная сила, соответствуюшая перемещению

Внешнее воздействие – температурное. Заменим в отличие от предыдущего индекс p на t . Тогда i - ое перемещение в стержневой системе от изменения температуры может быть определено как

,

где - внутренние усилия в системе, вызванные единичной силой, соответствующей по месту и направлению искомому перемещению, а - деформации удлинения, сдвига и изгиба, вызванные изменением температуры. Поскольку в статически определимых системах температурные воздействия не вызывают внутренних усилий, температурные деформации здесь являются свободными, т.е. нестесненными.

Для определения температурных деформаций рассмотрим элементарный участок стержня (рис. 7.8).

Будем полагать, что температура его изменилась по высоте поперечного сечения линейно от снизу до сверху, причем . Рассматриваемый отрезок стержня после изменения температуры принимает форму, показанную на рисунке штриховой линией. Удлинение нижнего волокна составит , верхнего - , а среднего по высоте - , где - коэффициент линейного расширения материала стержня. Деформация удлинения .

Изменение температуры, как видно из рисунка, не вызывает деформации сдвига, т.е. = 0.

Взаимный поворот поперечных сечений определяется как разность удлинений верхнего и нижнего волокон, деленная на высоту поперечного сечения, т.е. , откуда деформация .

Введя обозначения

и

соответственно, для температуры на оси стержня и градиента температуры по высоте поперечного сечения, получим

(7.8)

формулу Максвелла-Мора для определения перемещений в стержневой системе от изменения температуры. Для пользования этой формулой снова нужно рассмотреть два состояния: одно (вспомогательное) – под действием единичной силы, соответствующей по месту и направлению искомому перемещению, другое (основное) - под действием заданного изменения температуры. Во вспомогательном состоянии надо определить распределение внутренних усилий, а в основном – описать с помощью параметров и температурное поле.

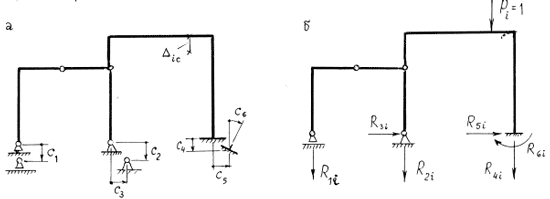
Внешнее воздействие – смещения опорных связей. Рассмотрим некоторую стержневую систему (рис. 7.9,а), опорные связи которой получили известные смещения … . Требуется определить вызванное этими смещениями перемещение .

Во вспомогательном состоянии (рис. 7.9,б) в стержневой системе под действием единичной силы, соответствующей по месту и направлению искомому перемещению, возникают опорные реакции ( их положительные направления согласованы с соответствующими смещениями) и внутренние усилия . Заменив в формуле (7.5) индекс k на c, получим

.

Поскольку рассматриваемая стержневая система является статически определимой, смещения опорных связей не вызывают в ней ни внутренних усилий, ни деформаций, т.е. . Следовательно, . В свою очередь работа внешних сил вспомогательного состояния (рис. 7.9,б) на соответствующих им перемещениях в основном состоянии

Для перехода к общему случаю обозначим: m - номер опорной связи (m = 1,2…n), - заданное смещение той же связи и - ее реакцию от единичной силы , соответствующей i - му искомому перемещению. Очевидно:

(7.9)

-формула Максвелла-Мора для определения перемещений в стержневой системе от заданных смещений связей.

Отметим, что произведения представляют собой работу и положительны только при совпадении направлений реакции и смещения; реакции во вспомогательном состоянии можно находить только для тех опорных связей, которые в основном состоянии получили заданные смещения.

Возможные упрощения формул Максвелла-Мора. Формула (7.7) получена с учетом всех деформаций, возможных в плоских стержневых системах. Но вклад разных деформаций в перемещения различен. Все три вида деформации (удлинение, сдвиг и изгиб) необходимо учитывать только в системах, составленных из относительно коротких (толстых) стержней. Если стержни относительно длинные (тонкие), то в большинстве случаев допустимо пренебрегать деформациями удлинения и сдвига, т.е. формула упрощается до

(7.10)

Деформации удлинения наряду с деформациями изгиба следует учитывать для рам из относительно длинных стержней в тех случаях, когда эти рамы вытянуты в каком-то одном направлении (например, в виде башни), а также при нагрузках, приложенных в основном вдоль осей стержней, и, наконец, в пологих арках (высотой менее 1/5 пролета).

В балках деформации удлинения вообще отсутствуют. Эти же деформации оказываются единственно возможными в шарнирных фермах.

Формула (7.8) упрощается только для тех стержневых систем, в которых тот или иной вид деформаций вообще не возникает (в балках нет деформаций удлинения, в фермах – деформаций изгиба).

Формула (7.9) и без того очень проста.

В универсальных программах расчета стержневых систем на ЭВМ проще учитывать все виды деформации.

7.5. Способы вычисления интегралов в формулах Максвелла-Мора

Из всех интегралов, входящих в формулы Максвелла-Мора, рассмотрим один

как наиболее общий.

Аналитический способ. Единственным требованием к участку интегрирования является непрерывность подынтегральной функции, т.е. ось стержня может быть прямолинейной и криволинейной, с постоянной или плавно изменяющейся жесткостью ЕI , а функции и - непрерывными и гладкими. Построение эпюр и не являются обязательным, но если они имеются, то о непрерывности и гладкости этих функций можно судить по отсутствию скачков и изломов на участке. В большинстве случаев аналитический способ наиболее трудоемкий, он может быть предпочтительнее только при расчете кольцевых систем.

Способ численного интегрирования. Требование к участку интегрирования здесь такие же, что и при аналитическом способе. В ряде случаев ради повышения точности результата вычислений может понадобиться разбиение участка на несколько интервалов. Из всех известных формул численного интегрирования наиболее удобной для задач строительной механики оказывается формула Симпсона:

Если подынтегральная функция на участке от a до b является многочленом до третьей степени включительно, формула Симпсона обеспечивает точный результат вычисления интеграла, так как погрешность формулы пропорциональна четвертой производной от подынтегральной функции.

Применяя формулу Симпсона к участку стержня длиной . Получим

,

(7.11)

где верхние индексы обозначают, что значения берутся в начале, середине и конце участка.

При постоянстве жесткости на протяжении участка формула (7.11) упрощается

(7.12)

Если стержень прямолинейный и с постоянной жесткостью, то точный результат получится при использовании этой формулы в случае, когда изменяется по линейному закону, а - по квадратичному ( т.е. момент вызван равномерно распределенной нагрузкой). Разумеется, точный результат вычислений по формуле (12) обеспечивается и при линейности обеих функций - и .

Если общее число участков интегрирования по длине всех элементов стержневой системы равно m , то

(7.13)

Покажем применение обоих способов интегрирования на примерах различных стержневых систем (будем полагать, что они составлены из относительно тонких стержней ).

П р и м е р 1. Требуется определить прогиб свободного конца консольной балки, изображенной на рис.7.10,а, находящейся под действием распределенной нагрузки q и сосредоточенного момента жесткость балки EI- const.

Отсчитывая абсциссу сечения x от свободного конца здесь можно обойтись без определения опорных реакций. Аналитические выражения изгибающих моментов в основном (рис. 7.10,а) и вспомогательном (рис. 7.10,б) состояниях балки таковы:

Знак моментов согласован с поставленным по нижней стороне пунктиром. Функции непрерывные и гладкие по всей длине балки, следовательно,

Положительное значение искомого перемещения, вычисленное аналитически , означает, что направлено в сторону действия единичной силы, т.е. вниз.

Применим теперь формулу Симпсона для вычисления значения интеграла. Предварительно построим эпюры и для основного и вспомогательного состояний балки (рис. 7.10,в и 7.10,г, соответственно). Очертание эпюр (отсутствие скачков и изломов, линейный характер изменения одной и параболический – другой) показывает, что на всей длине балки можно взять один участок интегрирования и получить точный результат. При этом безразлично, что считать за начало участка – левый или правый конец балки. Пусть начало будет слева, тогда :

.

П р и м е р 2. Требуется определить угол поворота и горизонтальное перемещение свободного конца стержня (рис.11,а), ось которого очерчена по дуге радиусом R . Жесткость стержня ЕI – const.

Кроме основного состояния (рис.7.11,а) необходимо рассмотреть два вспомогательных состояния (рис. 7.11,б,в) под действием единичных обобщенных сил, отвечающих искомым перемещениям. Выражения для функций изгибающих моментов в данном случае удобно получать в полярной системе осей координат:

Применив непосредственное интегрирование к формуле (7.10), получим:

Определим эти же перемещения по формуле Симпсона. Заметим, что подынтегральные функции в обоих случаях непрерывные и гладкие в пределах всей длины стержня, но сами функции не относятся к степенному полиному, поэтому без разделения длины стержня на несколько участков интегрирования точность результатов вычислений не гарантирована. Попробуем сначала принять весь стержень за один участок (пусть начало его соответствует , тогда середина ,конец- ):

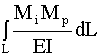
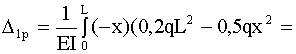
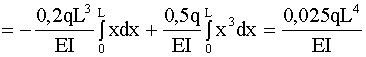
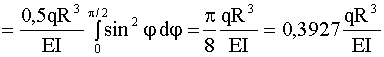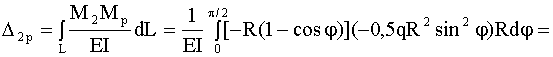
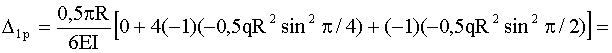
Как видно, значение первого перемещения не отличается от точного (вычисленного непосредственным интегрированием), а второе отличается от точного на 8% . Если разбить длину стержня на два участка интегрирования (их граница соответствует ), то получится , что всего на 0,2% отличается от точного значения.

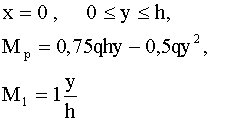
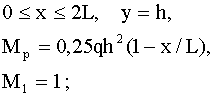
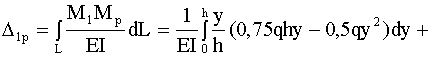
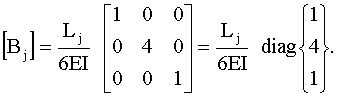
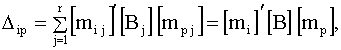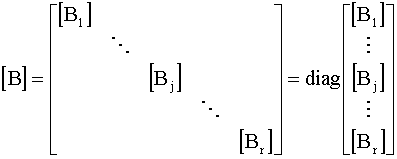
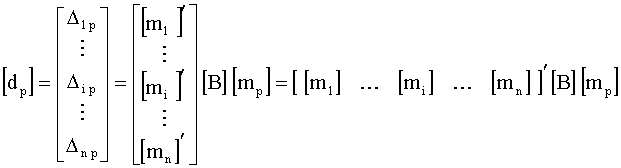
П р и м е р 3. Требуется определить угол раскрытия шарнира в раме, представленной на рис. 7.12,а, от распределенной нагрузки q.

Решим задачу cначала, применив аналитический способ интегрирования. Для этого в основном (рис. 7.12,а) и вспомогательном (рис. 7.12,б) состояниях необходимы аналитические выражения для и . После определения опорных реакций и выбора координатной системы получим:

Далее по формуле Максвелла-Мора получаем:

Выполнив интегрирование, найдем

Для выполнения вычислений по формуле Симпсона удобнее иметь не аналитические выражения и , а их эпюры (рис. 7.12,в,г). Будем обходить контур рамы, начиная с левой опоры. Наличие шарнира на ригеле не означает необходимость разделения ригеля на два участка, т.к. эпюры и отвечают требованиям непрерывности и плавности. Итак,

Нулевой результат интегрирования на ригеле можно было предвидеть, т.к. там эпюра антисимметричная, а - симметричная. "Умножение" симметричной и антисимметричной эпюр дает нулевой результат, если при этом и жесткость симметрична. Более того, можно заметить, что эпюра может быть разделена на две части: одна линейно очерчена и антисимметрична, а другая – параболическая с ординатой посередине, равной , эпюра - симметричная в целом. Следовательно, достаточно "умножить" параболическую часть эпюры на :

П р и м е р 4. Определим перемещение в шарнирной ферме на рис. 7.13,а от внешней нагрузки. Все стержни имеют одинаковое поперечное сечение и жесткость на удлинение ЕS .

Поскольку в стержнях фермы возникают только продольные усилия и продольные деформации, формула (7.7) Максвелла-Мора упрощается до

Постоянство функций в пределах каждого отдельного стержня фермы позволяет заменить интегрирование суммированием:

где j - номер стержня ( j = 1,2 …,n ), - - длина стержня, - продольные усилия в j - ом стержне от единичной силы, соответствующей i - му искомому перемещению, и от внешней нагрузки, соответственно.

В нашем случае i=1, j = 13 (нумерация стержней показана на рис. 7.13,а). Значения продольных усилий от внешней нагрузки и от единичной силы удобнее занести в таблицу. Для определения усилий в основном и во вспомогательном состояниях (рис. 7.13,а,б) сначала следует определить опорные реакции и выявить "нулевые" стержни (они на рисунке показаны), а затем применить способы вырезания узлов и сечений. Суммированием результатов в последней графе таблицы находим = 2,086 Ра / ЕS.

j
1			0,5	2P
2			0,5	2P
3			0,5	P	0,5
4			0,5	P	0,5
5					-
6			0	0	0
7			0	-	0
8				0	0
9	2		1	P	0,5
10				-	-
11			0	0	0
12			0	0	0
13				-

П р и м е р 5. Определим сближение точек А и В рамы на рис. 7.14 ,а от изменения температуры на 3t (нагрев) внутри и на – t (охлаждение) с внешней стороны. Все стержни рамы имеют одинаковое поперечное сечение высотой d. Для вычисления искомого перемещения по формуле (7.8)

Необходимо построить эпюры температурного градиента и температуры на оси стержня в основном состоянии. Эпюры и (рис. 7.14,б,в) построены по следующим правилам : ординаты откладываются на более теплой стороне стержня, а знак эпюры устанавливается так же как для эпюры изгибающего момента; эпюра строится аналогично эпюре продольной силы. Во вспомогательном состоянии рамы (рис. 7.14,г) от единичной обобщенной силы, соответствующей искомому перемещению, должны быть построены эпюры изгибающего момента и продольной силы (рис. 7.14,д,е).

Вычисления интегралов выполним по формуле Симпсона. При этом заметим, что все четыре эпюры симметричны относительно оси, проходящей через точки А и В, т.е. "перемножение" эпюр можно провести на любой половине рамы, например, верхней. Кроме того, эпюры и на стойках, соответственно антисимметричная и симметричная, т.е. для вычислений остается только ригельная часть этих эпюр. В свою очередь, на том же ригеле наблюдается симметрия эпюры и антисимметрия у эпюры . Итак,

П р и м е р 6. Определим угол поворота сечения в раме на рис. 7.15,а от заданных смещений опор. Согласно формуле (7.9) в основном состоянии (а это и есть то, что изображено на рис. 7.15,а ) не надо искать никаких усилий. Во вспомогательном состоянии (рис. 7.15,б) достаточно найти опорные реакции от единичной силы, отвечающей по месту и направлению искомому перемещению. Итак:

.

7.6. Матричная форма вычисления интегралов по формуле Симпсона

Матричный аппарат позволяет представить графическую информацию (эпюры и др.) массивами чисел (матрицами), тем самым упорядочить ее и весь расчет, а главное, - более эффективно использовать для расчета вычислительную технику.

Представим формулу (7.11) в матричной форме:

или

,

где

.

Если - const, то матрица упрощается до вида

Элементы главной диагонали этой матрицы представляют собой коэффициенты в формуле Симпсона.

Если общее число участков интегрирования равно r, т.е. j = 1, 2, … , r , то формула (7.11) может быть представлена так:

,

(7.14)

где

, ,

Матрицы – столбцы и имеют размер , а матрица - порядок, равный 3 r .

П р и м е р 7. Определим перемещение в раме на рис. 7.12,а , применив матричную форму записи информации и вычислений. Сохраним порядок обхода участков, принятый в примере 3, т.е. начиная с левой опоры. Матрица формируется блоками по исходным условиям (см. рис. 7.12,а), а и - по эпюрам (рис. 7.12,в,г):

, , .

, ,

Выполнив операцию над матрицами в соответствии с формулой , получим

Определение нескольких перемещений от одного внешнего воздействия.

Пусть требуется определить . Применяя к каждому из них выражение (7.14), найдем

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

или

Окончательно :

,

(7.15)

где .

Матрица [M] размером 3 r x n формируется столбцами из ординат эпюр , построенных от единичных обобщенных сил , соответствующих по месту и направлению искомым перемещениям .

Определение перемещений от нескольких сочетаний внешних воздействий.

Пусть требуется определить n перемещений от t внешних воздействий, рассматриваемых отдельно, т.е. нужно определить t векторов :

.

Согласно формуле (7.15),

,

или

(7.16)

где .

Матрица размером 3 r x t формируется столбцами из ординат эпюр , построенных от каждого из t заданных внешних воздействий.

П р и м е р 8. Определим в раме на рис.16,а горизонтальное перемещение правого верхнего узла (), сближение точек А и В () и угол раскрытия шарнира С () от сосредоточенной силы Р и распределенной нагрузки q , взятых отдельно. Пусть сила Р будет первым внешним воздействием, а нагрузка * - вторым.

Для вычислений по формуле (7.16) нужны эпюры изгибающего момента в трех вспомогательных состояниях (рис. 7.16,б-г) и в двух "грузовых" состояниях (рис. 7.16,д,е).

Рис. 7.16.

По очертанию всех пяти эпюр устанавливается число участков интегрирования так, чтобы на каждом участке все без исключения эпюры были непрерывными и гладкими: r = 6 (рис. 7.16,ж). Номера участков полезно снабдить указателями обхода этих участков, причем обход необязательно согласовывать с ранее выбранным пунктиром. Далее графическая информация представляется в матричной форме:

и окончательно:

Выполнив вычисления по формуле (7.16), получим: