Определение перемещений в статически определимых системах

7.1. Начало возможных перемещений для деформируемых систем

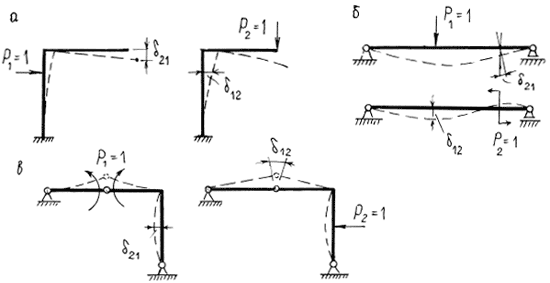
В курсе теоретической механики используется такая формулировка начала возможных перемещений: если система твердых тел, соединенных между собой жесткими связями, находится в равновесии под действием приложенных к ней внешних усилий, то при всяком возможном бесконечно малом перемещении точек этой системы сумма работ ее внешних усилий равна нулю. Возможные перемещения – это те, которые допускаются наложенными на систему связями.

Заметим, что эта формулировка применяется для системы твердых тел, т.е. недеформируемых (абсолютно жестких). Для деформируемых систем эта формулировка не применима, что видно из рис. 7.1.

В результате изгиба балки точки приложения внешних сил и перемещаются, соответственно, на и (они возможны, т.к. не противоречат связям, и малы по сравнению с размерами балки). Реакции в опорных связях перемещений не получат, и сумма работ . Если предположить, что балка недеформируемая, то и сумма работ окажется равной нулю.

В случае деформируемости системы необходимо учитывать работу внутренних усилий (эти же усилия возникают и в абсолютно твердых телах, но там работы они не совершают, поскольку отсутствуют деформации, на которых они могли бы совершить работу). Внутренние усилия в деформируемых системах препятствуют деформациям, не позволяя им расти бесконечно. То есть, когда внешние усилия совершают положительную работу на соответствующих перемещениях, внутренние усилия совершают отрицательную работу. При разгрузке системы от внешних усилий – все наоборот, т.е. внутренние усилия совершают положительную работу, возвращая систему в исходное до нагружения состояние.

Итак, начало возможных перемещений для деформируемых систем: если деформируемая система находится в равновесии под действием приложенных к ней внешних усилий, то при всяком возможном бесконечно малом перемещении точек этой системы (бесконечно малой деформации) сумма работ ее внешних и внутренних усилий равна нулю.

В связи с этой формулировкой начала возможных перемещений уточняется и понятие возможных перемещений: они не должны противоречить как внешним, так и внутренним связям в системе. Возможные перемещения необязательно должны быть бесконечно малыми – они могут быть малыми того же порядка, что и перемещения в рассматриваемых деформируемых системах при действии на них заданных внешних воздействий. Перемещения, вызванные заданными нагрузками, также являются возможными и их можно называть действительными или истинными.

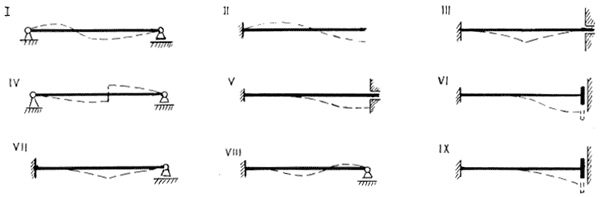
З а д а н и е . Указать, какие варианты изогнутой оси балки на рис. 7.2 не соответствуют понятию о возможном перемещении.

О т в е т: II (поворот сечения в заделке); IY (сдвиг) ; Y (вертикальное смещение скользящей заделки , допускающей только продольное смещение); YII (излом, т.е. взаимный поворот сечений, в месте, где отсутствует шарнир); IX (поворот сечения у скользящей заделки).

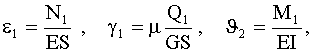
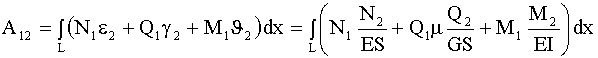7.2. Работа внешних и внутренних усилий на возможных перемещениях (деформациях)

Рассмотрим элементарный отрезок стержня (рис. 7.3,а.) в условиях плоской задачи под действием внешних нагрузок и (нагрузки действуют в плоскости , проходящей через ось стержня, а поперечное сечение стержня имеет плоскость симметрии, также совпадающую с плоскостью ).

Отрезок стержня находится в равновесии, т.е. внешние нагрузки и внутренние силы связаны между собой так:

(7.1)

Пусть отрезок стержня получает возможные перемещения (рис. 7.3,б), связанные не с нагрузками и , а с любым другим воздействием (например, с изменениями температуры). Чтобы подчеркнуть произвольность причины, вызвавшей эти перемещения, все концевые значения их отмечены *. Возможным перемещениям отвечают возможные деформации (на рис. 7.3,б пунктиром показана деформированная ось стержня, а на рис. 7.3,в – положительные направления угла поворота сечения , угла сдвига и изменения кривизны ). Деформации удлинения, сдвига и изгиба находятся по формулам сопротивления материалов, соответственно, как:

(7.2)

Обозначим работу внешних усилий на соответствующих им возможных перемещениях элементарного отрезка через . Внутренние усилия N,Q,M по концам стержня оказываются , как и нагрузки и , внешними по отношению к стержню, поэтому

.

Работа распределенных нагрузок определена здесь как работа их равнодействующих на осредненных значениях перемещений. После раскрытия скобок и пренебрежения малыми величинами второго порядка получим:

С учетом уравнений равновесия (7.1):

.

И, наконец, с учетом геометрических уравнений (7.2):

.

Для стержневой системы в целом

(7.3)

где L означает, что интегрирование осуществляется по длине всех стержней системы.

Работа внутренних усилий, которую обозначим через , может быть теперь найдена на основе начала возможных перемещений:

7.3. Теоремы о взаимности работ и взаимности перемещений

Введем предварительно понятия обобщенной силы и обобщенного перемещения. Рассмотрим некоторую совокупность разнообразных внешних усилий (рис. 7.4,а). Все эти усилия можно выразить через один параметр , который может иметь размерность любого усилия (сосредоточенной силы, распределенной нагрузки или момента). Если принять , то получится совокупность (рис. 7.4,б), в которой все усилия пропорциональны этому ( a и b имеют размерность длины).

Данную совокупность можно считать обобщенной силой, а параметр - значением этой силы (при =0 исчезают одновременно все составляющие обобщенной силы).

Пусть стержневая система вместе с приложенной к ней обобщенной силой получает возможное перемещение (штриховая линия на рис.7.4,в). Все составляющие обобщенной силы совершают работу на соответствующих им (по месту и направлению) возможных перемещениях:

.

Параметр , т.е. значение обобщенной силы, оказывается общим множителем в выражении работы. Работу, которая является скалярной величиной, можно представить в виде

,

где - обобщенное перемещение. Размерность получается делением размерности работы на размерность значения обобщенной силы. Применительно к примеру:

.

Как видно, обобщенное перемещение не есть просто сумма перемещений, на которых совершают работу составляющие обобщенной силы.

Понятия обобщенной силы и обобщенного перемещения позволяют оперировать произвольными совокупностями внешних усилий и различными сочетаниями перемещений так же просто, как одиночными силами и перемещениями.

Рассмотрим теперь одну и ту же стержневую систему, показанную, например, на рис. 7.5, под действием двух различных внешних нагрузок.

В первом состоянии в стержневой системе возникают внутренние усилия и деформации

А во втором состоянии – внутренние усилия и соответствующие деформации.

Определим работу, совершаемую внешними усилиями первого состояния на перемещениях, вызванных усилиями второго состояния, - . Эти перемещения являются действительными по отношению к усилиям второго состояния и могут приниматься в качестве возможных по отношению к усилиям первого состояния.
Полагая в формуле (7.3) и ,
получим

.

Аналогичным образом находится работа, совершаемая внешними усилиями второго состояния на перемещениях первого состояния:

.

Сопоставляя выражения и (первый индекс указывает на номер состояния, внешние усилия которого совершают работу, а второй – на номер состояния , на перемещениях которого совершается эта работа), находим

= ,

(7.4)

т.е. работа внешних усилий первого состояния на перемещениях второго состояния равна работе внешних усилий второго состояния на перемещениях первого (теорема взаимности работ Бетти).

Применим теперь понятие обобщенных сил и перемещений. Пусть внешние нагрузки первого состояния составляют обобщенную силу, значение которой , а нагрузки второго состояния составляют обобщенную силу и со значением . Тогда обе работы можно выразить через обобщенные перемещения:

и

(первый индекс у символа обобщенного перемещения указывает, какой обобщенной силе оно соответствует по месту и направлению, а второй – действием какой обобщенной силы вызвано.) С учетом равенства работ (7.4) получим

т.е обобщенное перемещение соответствующее первой единичной обобщенной силе и возникшее под действием второй единичной обобщенной силы, равно обобщенному перемещению, соответствующему второй единичной обобщенной силе и возникшему под действием первой единичной обобщенной силы – теорема о взаимности перемещений Максвелла.

Иллюстрацией теоремы о взаимности перемещений являются три примера на рис. 7.6. В случаях, когда обе обобщенные силы, имеют одинаковый характер (рис. 7.6,а, где и - сосредоточенные силы), соответствующие им обобщенные перемещения и одинаковы по значению и по размерности. Если обобщенные силы имеют разный характер (сосредоточенная сила и момент на рис. 7.6,б; два противоположно направленных момента и сосредоточенная сила на рис. 7.6,в), соответствующие им перемещения и равны только по значению, а размерности имеют разные – линейные перемещения измеряются в единицах длины, а угловые ( угол поворота сечения на рис. 7.6,б и взаимный угол поворота сечений или "угол раскрытия шарнира" на рис. 7.6,в) – в радианах.

Обобщая полученные результаты на случай, когда рассматриваемых состояний стержневой системы не два, а произвольное число, получим

(7.5)

и

,

(7.6)

где i и k - номера состояний стержневой системы.