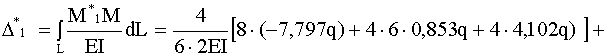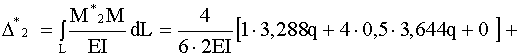|
|
Расчет статически неопределимых рам методом сил |
|
|
|
|
|
|
|
|
|
8.1 Основы метода сил |
Как определено в разделе 1.2, к статически неопределимым относятся те стержневые системы, для которых одних уравнений статики недостаточно для определения всех опорных реакций и внутренних усилий. Метод сил - один из основных методов расчета статически неопределимых систем, а название его связано с тем, что в разрешающую систему уравнений в качестве неизвестных входят усилия – реакции внешних и внутренних связей.
Общее число реакций связей складывается из
![]() реакций связей и
реакций связей и
![]() усилий в
усилий в
![]() замкнутых контурах, а общее число уравнений статики (равновесия) - из трех уравнений для плоской системы в целом и уравнений в виде условий отсутствия изгибающего момента в каждом одиночном шарнире. Отсюда находится степень статической неопределимости, т.е. число так называемых лишних связей (наложенных на систему сверх минимума, обеспечивающего геометрическую неизменяемость и статическую определимость):
замкнутых контурах, а общее число уравнений статики (равновесия) - из трех уравнений для плоской системы в целом и уравнений в виде условий отсутствия изгибающего момента в каждом одиночном шарнире. Отсюда находится степень статической неопределимости, т.е. число так называемых лишних связей (наложенных на систему сверх минимума, обеспечивающего геометрическую неизменяемость и статическую определимость):
![]() ,
,
где
![]() - суммарная краткость всех шарниров или, проще, число одиночных шарниров.
- суммарная краткость всех шарниров или, проще, число одиночных шарниров.
Усилия в лишних связях принято называть лишними неизвестными (лишними только в смысле невозможности их определения с помощью одних уравнений статики). Отметим, что без лишних связей стержневая система не имеет резерва для сохранения геометрической неизменяемости в случае разрушения хотя бы одной связи.
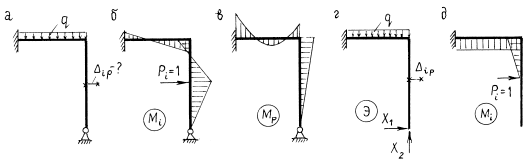
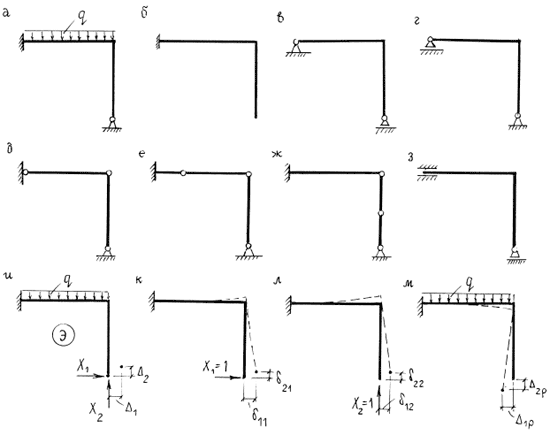
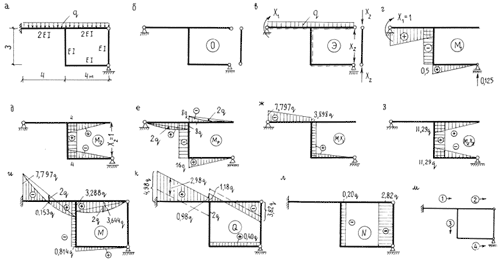
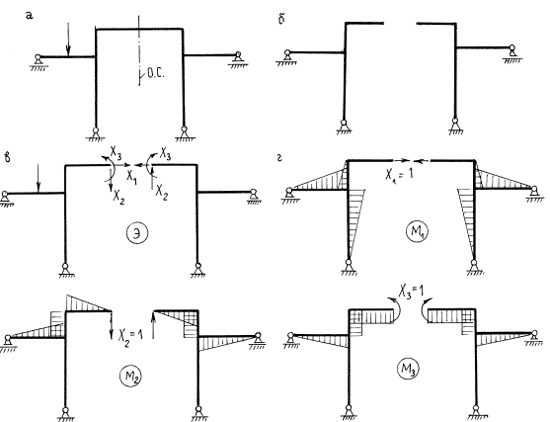
Метод сил базируется на использовании основной системы. Основная система – стержневая система, полученная из заданной системы путем отбрасывания лишних связей. Основная система должна быть обязательно геометрически неизменяемой. При удалении всех лишних связей она становится и статически определимой (применение статически неопределимых основных систем в принципе возможно, здесь же будем использовать только статически определимые основные системы). Из одной и той же заданной статически неопределимой системы можно образовать множество различных основных систем, удовлетворяющих требованиям геометрической неизменяемости и статической определимости. Рассмотрим для примера раму на рис. 8.1,а. Рама имеет две лишние связи:
![]() . Основную систему можно образовать либо устранением двух опорных связей (рис. 8.1,б-г), либо врезанием двух шарниров (рис. 8.1,д,е). Все эти варианты основной системы отвечают требованию геометрической неизменяемости, а вот варианты на рис. 8.1,ж,з – нет.
. Основную систему можно образовать либо устранением двух опорных связей (рис. 8.1,б-г), либо врезанием двух шарниров (рис. 8.1,д,е). Все эти варианты основной системы отвечают требованию геометрической неизменяемости, а вот варианты на рис. 8.1,ж,з – нет.
|
Идея метода сил вытекает из рассмотрения основной системы в состоянии эквивалентном тому, в котором находится исходная стержневая система под действием заданной нагрузки. Вернемся к примеру рамы на рис. 8.1. Воспользуемся вариантом основной системы, показанным на рис. 8.1,б. Приложим к основной системе заданную нагрузку q и реакции
![]() устраненных связей (рис. 8.1,и). Основная система под действием совокупности q ,
устраненных связей (рис. 8.1,и). Основная система под действием совокупности q ,
![]() должна быть эквивалентна исходной системе на рис. 8.1,а по распределению внутренних усилий, деформаций и перемещений, т.е. перемещения
должна быть эквивалентна исходной системе на рис. 8.1,а по распределению внутренних усилий, деформаций и перемещений, т.е. перемещения
![]() и
и
![]() по направлению устраненных связей должны быть равны нулю. Далее рассмотрим состояния основной системы под действием
по направлению устраненных связей должны быть равны нулю. Далее рассмотрим состояния основной системы под действием
![]() и внешней нагрузки (рис. 8.1,к-м). Используя принцип суперпозиции, можно получить условия для определения искомых значений
и внешней нагрузки (рис. 8.1,к-м). Используя принцип суперпозиции, можно получить условия для определения искомых значений
![]() :
:
![]() ,
,
![]() .
.
Обобщая этот результат на n раз статически неопределимую систему будем иметь
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
(8.1) |
Система (8.1) называется системой канонических уравнений метода сил. Любое i - ое уравнение системы отрицает перемещение основной системы, отвечающее по меcту и направлению искомому обобщенному усилию
![]() и вызванное совокупным действием искомых лишних неизвестных
и вызванное совокупным действием искомых лишних неизвестных
![]() и внешней нагрузки.
и внешней нагрузки.
Коэффициент
![]() означает перемещение, отвечающее усилию
означает перемещение, отвечающее усилию
![]() и вызванное действием
и вызванное действием
![]() . Свободный член
. Свободный член
![]() представляет собой перемещение, отвечающее усилию
представляет собой перемещение, отвечающее усилию
![]() , от действия внешней нагрузки. Все коэффициенты перед неизвестными и свободные члены уравнений в (8.1) – это перемещения в основной, т.е. статически определимой системе. Для их вычисления пригодны формулы и способы, приведенные в предыдущей главе.
, от действия внешней нагрузки. Все коэффициенты перед неизвестными и свободные члены уравнений в (8.1) – это перемещения в основной, т.е. статически определимой системе. Для их вычисления пригодны формулы и способы, приведенные в предыдущей главе.
Так, для рамы, составленной из относительно длинных стержней, можно пользоваться формулами
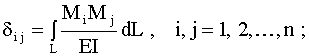

Если внешнее воздействие – температурное или в виде смещения опорных связей, то свободные члены вычисляются по формулам
![]() ,
,
![]() ,
,
cоответственно.
Отметим, что, независимо от вида внешнего воздействия, коэффициенты
![]() представляют собой перемещения от единичных усилий. При этом
представляют собой перемещения от единичных усилий. При этом
![]() , что следует из теоремы о взаимности перемещений, а
, что следует из теоремы о взаимности перемещений, а
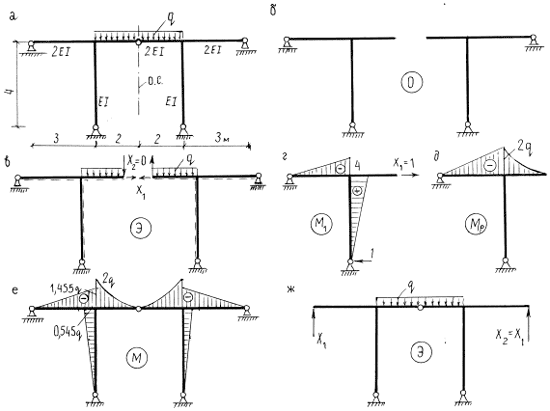
 .
.
Для вычисления всех коэффициентов и свободных членов системы уравнений метода сил необходимо предварительно получить эпюры (или функции)
![]() от
от
![]() и
и
![]() от внешней нагрузки.
от внешней нагрузки.
При температурном внешним воздействии кроме
![]() от
от
![]() необходимо
необходимо
![]() , а в случае задания смещения опор – реакции этих же опор от
, а в случае задания смещения опор – реакции этих же опор от
![]() .
.
По найденным в результате решения системы уравнений значением
![]() определяются окончательные ординаты изгибающего момента:
определяются окончательные ординаты изгибающего момента:
![]()
(при воздействиях в виде изменения температуры и смещения опор
![]() не существуют).
не существуют).
П р и м е р 8.1. Требуется построить эпюры внутренних усилий
![]() в раме (рис. 8.2,а), составленной из относительно тонких стержней. Рама содержит одну лишнюю связь
(
в раме (рис. 8.2,а), составленной из относительно тонких стержней. Рама содержит одну лишнюю связь
(![]() ). Основную систему можно образовать врезанием одного шарнира или удалением любой горизонтальной опорной связи (рис. 8.2,б). Для приведения основной системы в соответствие эквивалентное исходному, необходимо приложить к ней вместе с указанной нагрузкой реакцию удаленной связи
). Основную систему можно образовать врезанием одного шарнира или удалением любой горизонтальной опорной связи (рис. 8.2,б). Для приведения основной системы в соответствие эквивалентное исходному, необходимо приложить к ней вместе с указанной нагрузкой реакцию удаленной связи
![]() (рис. 8.2,в).
(рис. 8.2,в).
|
Система уравнений метода сил сводится в данном случае к одному уравнению
![]() , отрицающему горизонтальное перемещение правой опоры под действием искомого
, отрицающему горизонтальное перемещение правой опоры под действием искомого
![]() и заданной нагрузки. Далее строим эпюры
и заданной нагрузки. Далее строим эпюры
![]() от
от
![]() = 1 (рис. 8.2,г) и
= 1 (рис. 8.2,г) и
![]() от заданной нагрузки (рис. 8.2,д). Эпюра удобны при использовании формулы Симпсона для вычисления интегралов:
от заданной нагрузки (рис. 8.2,д). Эпюра удобны при использовании формулы Симпсона для вычисления интегралов:
|
|
Решая уравнение, находим

Окончательная эпюра изгибающего момента строится в соответствии с выражением
![]() (рис. 8.2,е), а по ней строятся эпюры Q и N (рис. 8.2,ж,з).
(рис. 8.2,е), а по ней строятся эпюры Q и N (рис. 8.2,ж,з).
П р и м е р 8.2. Требуется построить эпюры внутренних усилий
![]() в раме (рис. 8.3,а), составленной из относительно тонких стержней. Число лишних связей у рамы
в раме (рис. 8.3,а), составленной из относительно тонких стержней. Число лишних связей у рамы ![]() .
.
|
В замкнутом контуре вместо трех шарниров, необходимых для его статической определимости, имеется только два. Еще одна лишняя связь – среди опорных связей. Таким образом система один раз внутренне статически неопределима и один раз – внешне (см. раздел 1.2). При образовании основной системы (рис. 8.3,б) вместо постановки третьего шарнира в замкнутый контур выгоднее удалить простую связь в виде правой стойки, ограниченной по концам шарнирами, - это одновременно позволяет раскрыть контур и тем самым упростить последующее построение эпюр. Из четырех опорных связей может быть удалена любая одна кроме горизонтальной в защемлении. Здесь удалена связь, вызывающая момент, т.е. защемление превращено в шарнирную опору. Основная система в состоянии, эквивалентном исходному, показана на рис.8.3,в. При
![]() ,
,
![]() .
.
Первое уравнение отрицает поворот сечения в месте приложения
![]() , под воздействием искомых реакций удаленных связей
, под воздействием искомых реакций удаленных связей
![]() и
и
![]() , а также заданной нагрузки; второе уравнение отрицает расхождение точек приложения усилий
, а также заданной нагрузки; второе уравнение отрицает расхождение точек приложения усилий
![]() под теми же воздействиями.
под теми же воздействиями.
Далее строим эпюры
![]() ( от
( от
![]() = 1 ) ,
= 1 ) ,
![]() ( от
( от
![]() = 1 ) и
= 1 ) и
![]() от заданной нагрузки. Коэффициенты и свободные члены системы уравнений вычисляем по формуле Максвелла-Мора с использованием метода Симпсона при интегрировании:
от заданной нагрузки. Коэффициенты и свободные члены системы уравнений вычисляем по формуле Максвелла-Мора с использованием метода Симпсона при интегрировании:
|
|
Решая систему

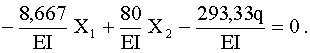
получим
![]()
Окончательная эпюра изгибающего момента получается с помощью выражения
![]() . Для удобства построения этой эпюры можно построить
. Для удобства построения этой эпюры можно построить
![]() и
и
![]() (рис. 8.3,ж,з). Окончательная эпюра
(рис. 8.3,ж,з). Окончательная эпюра
![]() показана на рис. 8.3,и. По ней строятся эпюры Q и N (рис. 8.3,к,л).
показана на рис. 8.3,и. По ней строятся эпюры Q и N (рис. 8.3,к,л).


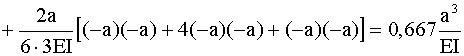 ;
; +
+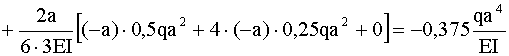 .
.
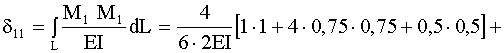

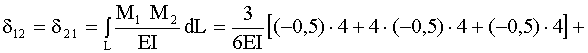


 ;
;
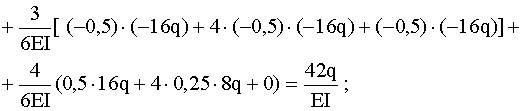


 ,
,
 ,
,
 .
.
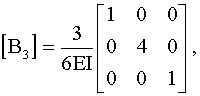

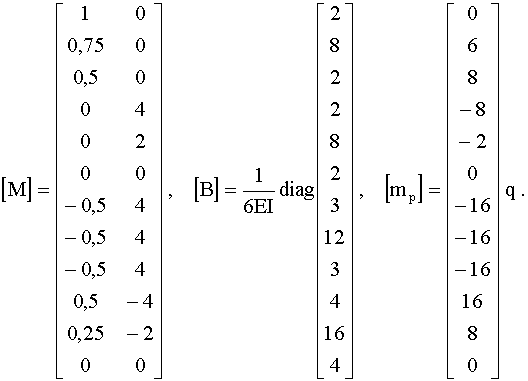


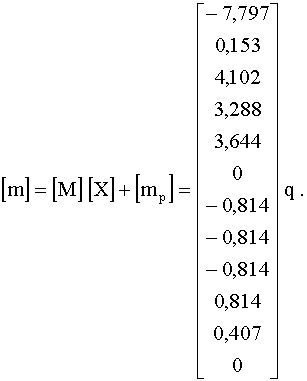
 и
и
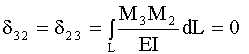 .
. ,
, , т.е.
, т.е.
 ,
,
 , т.е.
, т.е.
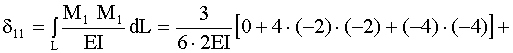
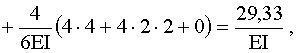
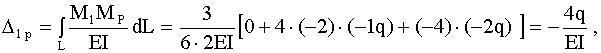

 .
.