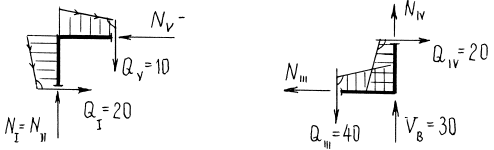4.3. Построение эпюр усилий в простейших замкнутых контурах

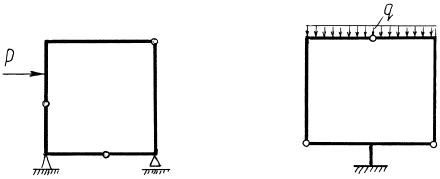
Простейший статически определимый замкнутый контур представляет стержневую систему вида ( рис. 4.9):

Как указывалось в разделе 1.2, подобные системы являются внешне и внутренне статически определимыми. Они также геометрически неизменяемые, если опираются на три связи, не параллельные и не пересекающиеся в одной точке, и не содержат трех шарниров на одной прямой.

Вычисление опорных реакций в системах с замкнутым контуром проводится традиционно, с использованием уравнений равновесия. В открытых рамах после нахождения опорных реакций строятся эпюры внутренних усилий на базе определений разделов 2.1 и 2.2. Особенность расчета контура заключается в том, что при нахождении внутренних усилий в сечениях контура, не удается посмотреть по одну сторону от сечения и воспользоваться определениями раздела 2.1, так как в замкнутой системе возвращаемся к сечению с другой стороны.

Выход заключается в том, чтобы превратить контур в открытую раму, разорвав его в некотором сечении. Затем, определив внутренние усилия в этом сечении, рассматривать их как внешние силы для образовавшейся рамы. Проще всего раскрыть контур по сечению с шарниром, так как здесь имеются только две составляющие внутреннего усилия , а в любом другом сечении – три. Для определения сил в одном из шарниров контура используются условия равенства нулю моментов в двух других шарнирах.

Рассмотрим примеры построения эпюр внутренних усилий в замкнутых контурах.

Задача 1. Построить эпюры внутренних усилий в стержневой системе, изображенной на рис. 4.10.

Статический расчет начинаем с вычисления составляющих опорных реакций, произвольно задавшись их направлением (рис. 4.10). Используем три уравнения равновесия. Составляем сумму проекций внешних сил на горизонтальную ось и определяем :

.

Далее записываем сумму моментов всех внешних сил относительно опорного шарнира А и находим :

.

Рассмотрев сумму проекций сил на вертикальную ось, получим значение :

.

Приложим к контуру найденные силы, заменив принятые направления векторов и на противоположные (рис. 4.11). Рассечем контур по шарниру D (рис.4.11). Возникает вопрос, к какой части сечения отнести силу P, приложенную в шарнире.

З а м е ч а н и е. Когда внешняя сила действует в рассекаемом сечении, она разносится между двумя образовавшимися точками произвольно. Но так, чтобы в сумме две новые силы давали бы исходную. Если сила P действует в сечении на оси симметрии системы, то при рассечении рамы по оси симметрии к обеим частям прикладываются силы, равные P/2. Это позволяет сохранить симметрию задачи. В общем случае часто внешнюю силу в рассекаемом сечении целиком относят к одной части сечения.

В рассматриваемой задаче отнесем силу P к нижнему сечению ( рис. 4.11) и зададимся направлением составляющих и внутренней силы в шарнире D. Для определения и воспользуемся равенством нулю моментов в шарнирах E и C. При записи выражений для моментов в точках E и C, согласно определению раздела 2.1, смотрим по одну сторону от сечения.

Рис. 4.11.

Вычтем первое уравнение из второго и

найдем :

Из первого уравнения определим : .

После раскрытия контура и вычисления сил в шарнире D для построения эпюр внутренних усилий можно применить стандартные приемы, описанные в разделах 2.1, 2.2, 4.1. Выделим в системе пять незагруженных участков: I-V и отметим сечения 1 - 6 на границах участков (рис. 4.11). Из дальнейших рассуждений будет ясно, что для построения эпюры M, достаточно определить моменты в сечениях 1 и 2 (рис. 4.12):

Отложив в сечениях полученные ординаты со стороны растянутых волокон и учитывая, что , строим линейные эпюры на I и II участках (рис. 4.13).

В сечение 3 III участка момент определяется из условия моментного равновесия узла с сечениями 2 и 3 (рис. 4.13). Строится линейная эпюра M на III участке от ординаты 80 в сеч. 3 через нуль в шарнире С до сеч. 4. Здесь значение момента, равное 80, определяется из подобия треугольников эпюры.

В сечение 5 момент на эпюре графически переносится из сеч. 4 по условию моментного равновесия узла. Изображается линейная эпюра на IV участке от ординаты в сечении 4 до нуля в шарнире Е.

Аналогично, из условия равновесия узла, определяется значение момента в сеч. 6 и строится линейная эпюра M на V участке (рис. 4.13).

Отметим, что моментное равновесие всех узлов рамы обеспечивалось в процессе построения эпюры M. Проводим пунктир, расставляем знаки ординат эпюры моментов (см. 2.1).

Значения ординат эпюры Q находим по формуле (2.2). Эпюра и вычисления приведены на рис. 4.14.

Рис. 4.14.

Продольные силы в стержнях контура определяем из силовых уравнений равновесия, записанных для левого верхнего и правого нижнего узлов (рис. 4.15).

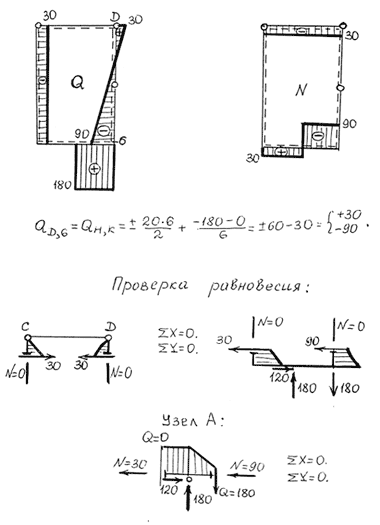
Эпюра N показана на рис. 4.16.

Можно проверить, что полученные эпюры Q и N будут теми же, если их ординаты вычислять как алгебраическую сумму проекций сил, действующих по одну сторону от сечения.

В системах с контурами после построения эпюр внутренних усилий обязательно проводится горизонтальное (лучше и вертикальное) сечение и проверяется силовое равновесие отсеченной части рамы. Проведем сеч. 1 – 1 и 2 – 2, показанные на рис. 4.10 и рассмотрим равновесие частей рамы под действием внешних и внутренних сил (рис. 4.17).

Задача 2. Осуществить статический расчет системы, представленной на рис.4.18.

Рис. 4.18.

Находим опорные реакции:

В случае, когда два шарнира контура лежат на одной вертикали или горизонтали, то рассекать контур лучше по одному из этих шарниров. Это упростит нахождение внутренних сил в шарнире. Раскроем данный контур по шарниру Е (рис.4.19).

Рис. 4.19.

Составляющая может быть сразу найдена, момента в противоположном шарниру Е шарнире С:

Теперь определим :

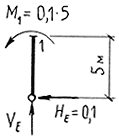
Перед построением эпюры M отметим, что на всех стержнях контура эпюра M должна быть линейна, так как стержни не загружены. Приложенные моменты создают в сечении С момент, равный единице (рис. 4.20). Для построения эпюры M достаточно определить ординату в сеч. 1 (рис. 4.21).

Рис. 4.20.

Рис. 4.21.

Отложим ее в сечении со стороны растянутых волокон и коротко прокомментируем процесс построения эпюры моментов (рис. 4.22).

Рис. 4.22.

На правой стойке прямая эпюры проводится через ординату 0,5 в сеч.1 и нуль в шарнире Е. При этом ордината в нижнем сечении стойки оказывается равной также 0,5. Из условия моментного равновесия узла переносим ординату в правое сечение верхнего ригеля (горизонтального участка). Через нее и нулевую ординату в шарнире D строим линейную эпюру. В левом сеченииверхнего ригеля получаем значение момента 0,5 со стороны нижних волокон. На левой стойке ординату эп. M в верхнем сечении определяем из равновесия узла. Линейная эпюра проводится через эту точку и равную единице ординату в сеч. С. Тогда значение момента в нижнем сечении левой стойки равно 1,5. В крайних сечениях нижнего ригеля моменты находятся из условий моментного равновесия узлов. Две ординаты 1,5 и 0,5 определяют линейную эпюру на участке. Построение эпюры M закончим изображением пунктира со стороны внутренних волокон контура и расстановкой знаков ординат по правилам раздела 2.2. (рис. 4.22).

Эпюры Q и N в данной задаче довольнопросто могут быть построены по аналогии с эпюрами в предыдущей задаче.

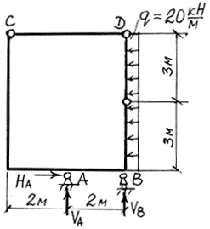
Задача 3. Рассмотрим еще один часто встречающийся случай, когда контур включает незагруженный стержень с шарнирами на концах (рис. 4.23).

Рис. 4.23.

Определяем, как обычно, опорные реакции, используя три уравнения равновесия для всей системы:

Далее необходимо рассечь контур по одному из шарниров и найти в нем внутренние силы. В данном случае вычисления упростятся, если сечение провести по шарниру C или D. Для пояснения сказанного выделим стержень CD из системы: (рис. 4.24):

На стержень действуют две силы, приложенные в шарнирах. Под действием двух сил стержень может находиться в равновесии, если силы равны по величине, противоположны по направлению и действуют по одной прямой. Следовательно, в рассматриваемом стержне возникают только продольные усилия.

Рассечем контур по шарниру С и найдем внутреннюю силу , используя условие равенства нулю момента в шарнире Е (рис. 4.25).

Рис. 4.25.

Далее строим эпюры внутренних усилий по методике, описанной в разделах 4.1 и 2.5. Выделяем в контуре четыре участка: I – IV (рис.4.25). На незагруженных участках линейная эпюра M строится по двум ординатам, вычисленным на рис. 4.25 в крайних сечениях участков и отложенным со стороны растянутых в сечениях волокон. На IV участке, где действует нагрузка q, одна из ординат эп. M в крайнем сечении определяется переносом из сеч. 5 по условию моментного равновесия жесткого узла. Другая ордината равна нулю (момент в шарнире D). Следуя методике, изложенной в разделе 2.5, строим на участке квадратичную параболу эпюры M (рис. 4.25). Проводим пунктир и ставим знаки на эпюре M (раздел 2.2).

Для построения эпюр Q и N величины перерезывающих и продольных сил в сечениях могут быть найдены из рассмотрения условий равновесия частей рамы по одну сторону от сечения (рис. 4.26). Кроме того, ординаты эп.Q могут быть вычислены на незагруженных участках по формуле (2.2), а на участке с равномерно распределенной нагрузкой – по формуле (2.3). На рис. 4.26 по формуле (2.3) определены ординаты эпюры Q в крайних сечениях участка IV.

В заключении расчета строим эпюру N по найденным в сечениях значениям продольных сил и проводим проверку равновесия частей рамы и узла А (рис. 4.26).

Рис. 4.26.