Статически определимые арки

5.1 Общие понятия и определения

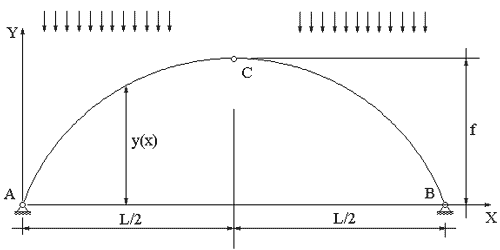
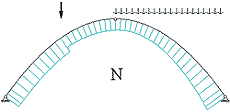
Арка - система криволинейных стержней. К статически определимым системам относятся трехшарнирные арки, имеющие шарнирные опоры на краях и один промежуточный шарнир, чаще всего - центральный (рис. 5.1).

Пролет арки - расстояние между ее опорами L. Опору арки принято также называть пятой арки, центральный шарнир - замком арки, а расстояние f от прямой, соединяющей опорные шарниры до замка арки, - стрелой арки или стрелой подъема арки.

Арки относятся к распорным системам, т.е. таким системам, в опорах которых, в отличие от безраспорных систем, при действии только вертикальной нагрузки возникает ненулевое горизонтальное усилие, называемое распором.

Инженер-строитель может столкнуться с необходимостью выбора между безраспорной системой (балкой) и распорной системой (аркой) для выполнения перекрытия некоторого пролета, например, мостового. При этом арку сопоставляют с соответствующей балкой, т.е. простой балкой на двух опорах, перекрывающей такой же пролет и находящейся под действием такой же вертикальной нагрузки, что и арка.

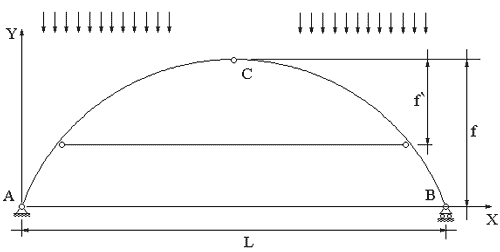
Частным случаем трехшарнирной арки является трехшарнирная арка с затяжкой (рис. 5.2).

Затяжка - горизонтальный стержень, предназначенный для полного или частичного восприятия горизонтального распора. Для того, чтобы система при наличии затяжки осталась статически определимой, одну опору арки делают катковой. В этом случае, при отсутствии горизонтальной составляющей нагрузки горизонтальные реакции в опорах будут равными нулю, а затяжка будет воспринимать распор полностью.

При нагрузке определенного вида очертание арки можно задать таким, чтобы в ней не возникало изгибающих моментов. Такие арки называют арками рационального очертания.

Задание геометрии арки.

При задании геометрии арки необходимо определить величины пролета L, стрелы f, и функцию y(x), описывающую очертание оси арки (рис. 5.1). Для арки с затяжкой, кроме того, необходимо задать высоту над затяжкой f’ (рис. 5.2).

Задав значения L и f, мы определяем положение трех точек - опор и замка арки. Если дополнительно потребовать, чтобы ось арки была очерчена по окружности или по параболе, то положение этих трех точек однозначно определит функцию y(x), поскольку через три точки можно провести только одну окружность и только одну параболу.

При круговом очертании арки:

, где ,

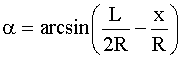(5.1).

При параболическом очертании арки:

,

(5.2).

Угол в (5.1) и (5.2) - угол наклона касательной к оси арки в данной точке (рис.5.1). На левой половине арки , на правой - . Справедливость формул (5.1) и (5.2) читателю предлагается проверить самостоятельно.

Понятно, что ось арки может быть очерчена не только по параболе или окружности.

5.2. Статический расчет трехшарнирной арки

В принципиальном отношении расчет трехшарнирной арки не отличается от расчета других статически определимых систем: вначале определяются опорные реакции, затем строятся эпюры изгибающего момента, продольного и перерезывающего усилия, после чего выполняются проверки и, при необходимости, определяются перемещения. Единственная особенность, с которой приходится сталкиваться, - появление чисто вычислительных трудностей, связанных с криволинейностью очертания оси арки.

Как в любой статически определимой системе, реакции в опорах трехшарнирной арки находятся исключительно из статических уравнений (уравнений равновесия). Примем положительные направления реакций в опорах арки в соответствии с рис. 5.3.

Из условия равенства нулю суммы проекций всех действующих на систему сил на вертикальную ось имеем:

,

(5.3)

где - сумма проекций всех действующих на арку внешних сил на вертикальную ось. В (5.3) внешняя сила считается положительной, если она направлена вниз.

Далее, составим уравнение моментов всех действующих на систему сил относительно произвольной точки. Здесь в качестве точки, относительно которой будут вычисляться моменты, выберем точку А. Поскольку линии действия трех опорных реакций из четырех проходят через эту точку, в уравнении останется только одна неизвестная реакция - V_B:

,

(5.4)

где -суммарный момент действующих на систему внешних сил относительно точки А. В (5.4) он считается положительным, если направлен по часовой стрелке.

Уравнений (5.3) и (5.4) достаточно, чтобы найти вертикальные реакции в опорах арки. Составив аналогичные уравнения для балки, соответствующей арке (рис. 5.3), легко убедиться, что при отсутствии горизонтальной составляющей нагрузки эти уравнения совпадут с (5.3) и (5.4), а значит вертикальные реакции V_A и V_B в опорах арки и соответствующей ей балки будут одинаковыми.

Из условия равенства суммы проекций всех действующих на систему сил на горизонтальную ось имеем:

,

(5.5)

где - сумма проекций действующих на арку внешних сил на горизонтальную ось. В (5.5) внешняя сила считается положительной, если она направлена вправо.

Четвертое уравнение - условие равенства нулю суммы моментов всех сил, действующих на систему с одной (любой- левой или правой) стороны от промежуточного шарнира относительно этого шарнира. Рассмотрим, например, равновесие левой половины арки:

,

(5.6)

где - суммарный момент действующих на левую часть арки внешних сил относительно точки С. В (5.6) в качестве его положительного направления принято направление против часовой стрелки.

При отсутствии горизонтальной составляющей внешней нагрузки горизонтальные реакции в опорах арки будут равны и направлены противоположно друг другу, что следует из уравнения (5.5):

.

(5.7)

Горизонтальное усилие H, возникающее в опорах, называется распором.

Из уравнений (5.3)-(5.6) можно найти четыре неизвестные опорные реакции , после чего приступить к определению изгибающих моментов в сечениях арки.

Рассмотрим сечение, находящееся на произвольном расстоянии х от левой опоры арки (рис. 5.3). Рассматривая равновесие части арки с одной стороны от данного сечения, найдем в нем изгибающий момент. Будем рассматривать часть арки слева от сечения. Тогда

,

(5.8)

где - изгибающий момент в рассматриваемом сечении, вызванный исключительно внешними силами, действующими слева от рассматриваемого сечения.

Как мы уже выяснили, при отсутствии горизонтальной составляющей нагрузки вертикальные опорные реакции в арке и в соответствующей ей балке будут одинаковыми, а горизонтальные реакции в опорах арки равны и противоположно направлены. Изгибающий момент в балке определяется по формуле . Сопоставляя эту формулу с (5.8), с учетом (5.7) получим:

(5.9)

Таким образом, при условии отсутствия горизонтальной составляющей нагрузки, зная распор в арке и изгибающий момент в любом сечении балки, соответствующей рассматриваемой арке, момент в этом же сечении арки можно найти и по формуле (5.9).

Для определения продольного и перерезывающего усилий рассмотрим сечение в арке, отстоящее от левой опоры на произвольное расстояние х (рис.5.3).

Перерезывающее усилие в арке действует перпендикулярно ее оси в данном сечении, а продольное - вдоль ее оси в данном сечении (рис.5.4). Обозначим сумму проекций всех внешних сил и реакций опор, действующих на рассматриваемую часть сечения, на вертикальную и горизонтальную оси и соответственно. Положительными направлениями этих сил будем считать такие направления, которые будут уравновешиваться положительными Q^арк(x) и N^арк(x) на оси арки (рис.5.5). Составив уравнения равновесия сил, действующих на рассматриваемую часть сечения в осях, совпадающих с направлением действия и (рис.5.6) получим выражения для определения перерезывающего и продольного усилия:

;

(5.10)

(5.11)

Рис. 5.5.

Рис. 5.6.

При определении опорных реакций и распора в таких арках затяжку мысленно удаляют, заменяя ее действие на остальную часть конструкции усилиями H (рис.5.7).

Далее составляют обычные уравнения равновесия, которые в этом случае примут вид:

		(5.12)
,		(5.13)
,		(5.14)
.		(5.15)

Если далее рассматривать распор в затяжке Н как одну из внешних нагрузок (рис.5.7), то построение эпюр внутренних усилий можно выполнить аналогично арке без затяжки по формулам (5.8), (5.10) и (5.11).

5.3. Пример расчета арки параболического очертания под действием вертикальной нагрузки

Рассмотрим арку параболического очертания, изображенную на рис. 5.8.

Определим опорные реакции в арке, для чего запишем систему статических уравнений (5.3)-(5.6):

Из второго уравнения находим:

= .

Далее, из первого уравнения найдем

.

И, наконец, найдем распор

.

Для проверки правильности найденных опорных реакций составим, например, уравнение моментов сил, действующих справа от промежуточного шарнира, относительно этого шарнира:

Таким образом, опорные реакции определены, приступаем к построению эпюры изгибающего момента, для чего используем формулу (5.8). Все расчеты сведем в таблицу 5.1.

Таблица 5.1.

x, м	, кНм	y(x), м	, кНм
1	2	3	4
0	0	0	0
2,5	0	3,0625	-31,25
5	0	5,25	25
7,5	-200	6,5625	-31,25
10	-400	7	0
12,5	-662,5	6,5625	56,25
15	-1050	5,25	75
17,5	-1562,5	3,0625	56,25
20	-2200	0	0

Покажем, как определяется , например, в сечении с координатой x=15м. Рассматривая часть арки слева от сечения (рис.5.9), видим, что изгибающий момент от действия внешних нагрузок складывается из моментов от действия силы Р с плечом 10 м и действующей на длине 5 м распределенной нагрузки q, равнодействующая которой создает в рассматриваемом сечении момент с плечом 2,5 м. Оба момента создают растяжение верхних волокон арки в рассматриваемом сечении, поэтому имеют знак "минус".

Итак,

.

После определения изгибающих моментов от внешней нагрузки в выбранных сечениях (заполнения столбца 2), приступаем к определению в этих же сечениях значений y(x) (столбец 3) и изгибающих моментов в арке (столбец 4). Если во всех сечениях моменты определяются из рассмотрения равновесия части арки с одной и той же стороны от сечения (в нашем случае - с левой стороны), последние две операции для всех сечений выполняются по однотипным формулам. Следовательно, эти вычисления легко автоматизировать, например, с помощью табличных процессоров. Если в замке или в опоре арки изгибающий момент в результате расчета окажется отличным от нуля, то это будет говорить о допущенной ошибке.

Эпюра изгибающего момента в арке приводится на рис.5.10.

Построим теперь эпюры продольного и перерезывающего усилий, для чего воспользуемся формулами (5.9) и (5.10). Поскольку горизонтальная составляющая нагрузки отсутствует, при любом х. Все расчеты легко автоматизируются, например, при помощи табличного процессора. Результаты расчетов сведены в таблицу 5.2.

Таблица 5.2.

x, м	, кН	, радианы	, кН	, кН
1	2	3	4	5
0	110	0,950547	-17,437	-147,635
2,5	110	0,809784	3,448	-148,621
5-0	110	0,610726	32,769	-145,004
5+0	30	0,610726	-32,769	-99,127
7,5	30	0,336675	-4,719	-104,296
10	30	0	30	-100
12,5	-20	-0,336675	14,158	-100,993
15	-70	-0,610726	0	-122,066
17,5	-120	-0,809784	-10,345	-155,862
20	-170	-0,950547	-17,437	-196,459

Эпюры перерезывающего и продольных усилий в арке приведены на рис.5.11 и рис.5.12.

Рис. 5.10.

Рис. 5.11.

Рис. 5.12.

Обратите внимание, что на оси арки продольное усилие равно распору, а перерезывающее - перерезывающему усилие в соответствующей ей балке.

5.4. Пример расчета арки кругового очертания под действием горизонтальной нагрузки

Рассмотрим полукруглую арку, изображенную на рис. 5.13.

Опорные реакции в арке определяются из уравнений равновесия (5.3)-(5.6):

Решая эту систему, находим: , , , .

Для проверки правильности найденных опорных реакций составим, например, уравнение моментов сил, действующих слева от промежуточного шарнира, относительно этого шарнира:

Обратите внимание, что при наличии горизонтальной нагрузки, горизонтальные реакции в обеих опорах арки в общем случае не равны.

При определении изгибающего момента, продольного и перерезывающего усилий в полукруглой арке положение сечений удобно задавать углом . Он будет меняться в пределах от 90⁰ до -90⁰ (рис. 5.13). Как и в предыдущей задаче, будем рассматривать равновесие левой от сечения части арки (рис. 5.14, 5.15).

Рис. 5.14.

Рис. 5.15.

Момент от действия внешней нагрузки будет равен

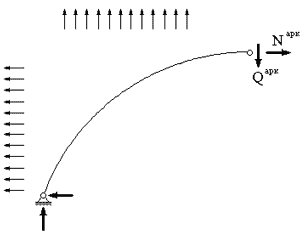
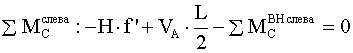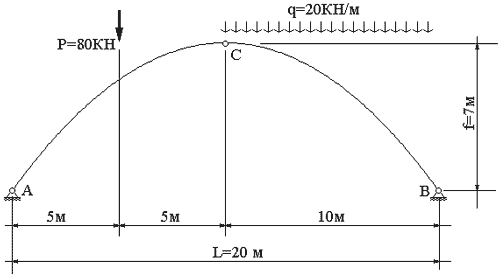
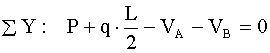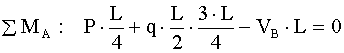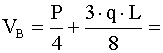
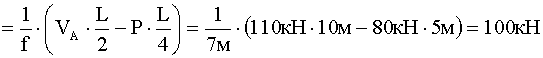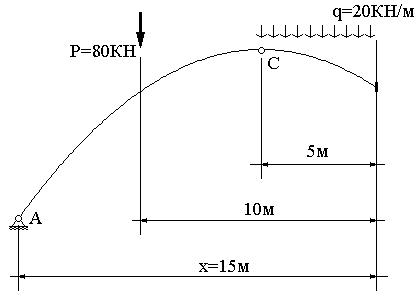
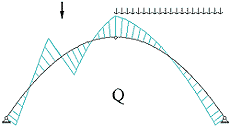
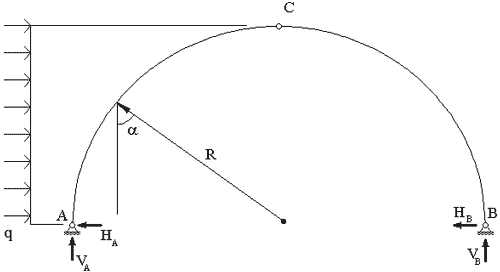
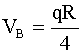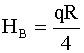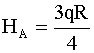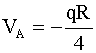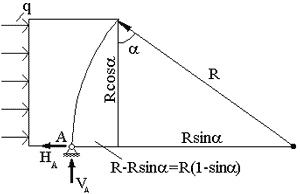
- для левой половины арки,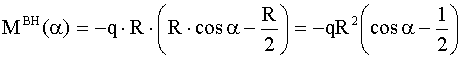

-для правой половины арки.

Значения и определяются по формулам и , выражение для изгибающего момента принимает вид (рис. 5.14, 5.15). Все расчеты легко автоматизируются, например, при помощи табличного процессора. Результаты расчетов сведены в таблицу 5.3.

Таблица 5.3.

, градусы	, ,	x()	y()
1	2	3	4	5
90	0	0	0	0
75	-0,033	0,034R	0,259R	0,152
60	-0,125	0,134R	0,5R	0,217
45	-0,25	0,293R	0,707R	0,207
30	-0,375	0,5R	0,866R	0,150
15	-0,467	0,741R	0,966R	0,073
0	-0,5	R	R	0
-15	-0,466	1,259R	0,966R	-0,056
-30	-0,366	1,5R	0,867R	-0,092
-45	-0,207	1,707R	0,707R	-0,103
-60	0	1,867R	0,5R	-0,092
-75	0,241	1,966R	0,259R	-0,056
-90	0,5	2R	0	0

Эпюра изгибающего момента в данной арке приведена на рис.5.16.

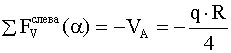Теперь по формулам (5.9) и (5.10) построим эпюры продольного и перерезывающего усилий. Поскольку вертикальная нагрузка на арку отсутствует, значение для любого . Значение определяется по формулам (рис.5.14, 5.15):

- для левой половины арки,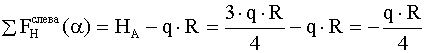

- для правой половины.

Все расчеты легко автоматизируются, например, при помощи табличного процессора. Результаты расчетов сведены в таблицу 5.4.

Таблица 5.4.

, градусы
1	2	4	5
90	0,750	0,750	0,250
75	0,491	0,410	0,369
60	0,250	0,092	0,342
45	0,043	-0,146	0,207
30	-0,116	-0,275	0,025
15	-0,216	-0,297	-0,144
0	-0,250	-0,25	-0,25
-15	-0,250	-0,177	-0,306
-30	-0,250	-0,092	-0,342
-45	-0,250	0	-0,354
-60	-0,250	0,092	-0,342
-75	-0,250	0,177	-0,306
-90	-0,250	0,250	-0,250

Эпюры перерезывающего и продольных усилий в арке приведены на рис. 5.17 и рис.5.18.

Рис. 5.16.

Рис. 5.17.

Рис. 5.18.