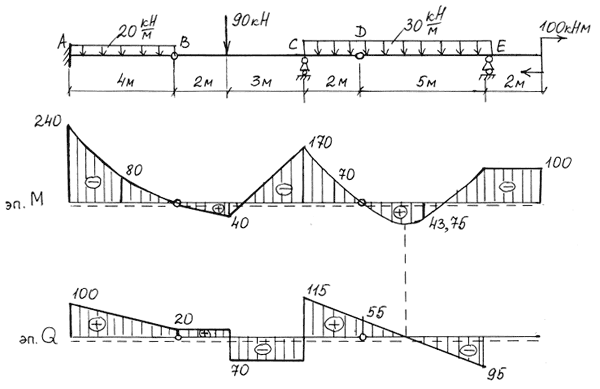
Шарнирные балки

3.1. Образование шарнирных балок

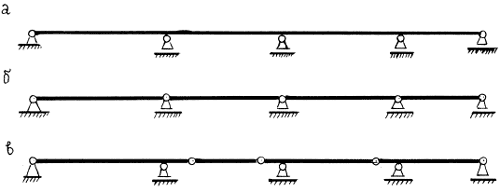
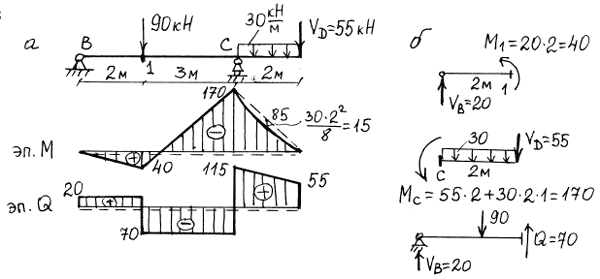
Если требуется перекрыть балкой большой пролет, часто приходится ставить промежуточные опоры. При этом получается статически неопределимая неразрезная балка (рис. 3.1,а). Если в такой балке поставить шарниры над промежуточными опорами, то получится цепочка статически определимых простых балок (рис. 3.1,б). Каждую из балок можно рассчитать от нагрузки на ней расположенной. Реакции промежуточных опор в таком случае были бы равны алгебраической сумме реакций со стороны двух соседних с этой опорой простых балок, изгибающие моменты на опорах были бы равны нулю.

Можно поступить иначе, поставив шарниры не над опорами, а в пролетах балок (рис. 3.1,в). Полученная система является по-прежнему статически определимой и называется шарнирной балкой.

Как будет показано ниже, изгибающие моменты на промежуточных опорах таких балок не равны нулю, но зато изгибающие моменты в пролетах меньше, чем в соответствующих сечениях простых балок. Подобное перераспределение целесообразно, так как размеры поперечных сечений балок выбираются в зависимости от наибольших значений изгибающих моментов.

Шарниры в пролетах ставятся с учетом нагрузки, величины пролетов и других факторов. Общее количество шарниров находится из условия статической определимости балки, когда =0. Из (1.1), учитывая, что контуров в балках нет, имеем:

(3.1).

Непременным условием правильной расстановки шарниров является геометрическая неизменяемость шарнирной балки. Последнюю легко проверить, если изобразить шарнирную балку в виде звеньев, опирающихся друг на друга и на опоры. Такое представление балки называется этажной схемой балки. Звено балки – участок балки между шарнирами.

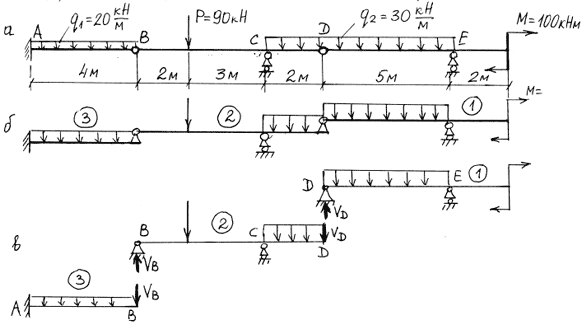
Рассмотрим балку, изображенную на рис. 3.2,а. Условие статической определимости балки выполняется, так как по формуле (1.1) имеем : (в балке контуров нет и ). Для проверки правильности расстановки шарниров построим этажную схему балки (рис. 3.2,в).

Построение ее начинаем со звена балки, имеющего три опорные связи (опоры А и В). Следующее за ним справа звено не имеет собственных опор и должно поддерживаться соседними звеньями. Каждый шарнирный узел эквивалентен двум связям, в которых возникают два внутренних усилия ( ). Такой узел изображается как шарнирная неподвижная опора. Третье звено, имеющее одну опорную связь (опору С), подводим под второе звено. Крайнее справа звено должно поддерживать третье, как имеющее только одну опорную связь. Осталось убедиться в неподвижности последнего звена: оно имеет две вертикальные опорные связи. Невозможность горизонтальных перемещений этого звена обеспечивается наличием цепочки всех остальных звеньев, прикрепленных к неподвижной опоре А.

Для балки на рис. 3.3,а =5-3-2=0. При построении этажной схемы можно сразу заметить, что крайнее слева звено балки имеет четыре опорные связи (заделку и катковую опору) вместо трех, достаточных для его закрепления. Это приводит к тому, что в другой части балки связей недостаточно. А именно, построение этажной схемы (рис. 3.3,б) показывает, что крайнее справа звено с одной опорной связью подвижно и не может поддерживать слева соседнее звено, вообще не имеющее собственных опор. Таким образом, балка содержит геометрически изменяемые элементы, следовательно, шарниры в ней расставлены не верно.

Перечислим основные правила постановки шарниров:

Следуя этим правилам расстановку шарниров в балке на рис. 3.3,а нужно изменить так, как показано на рис. 3.3,в.

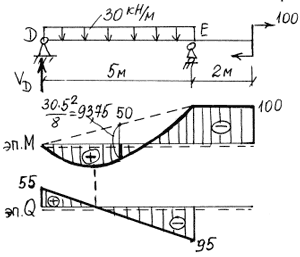
3.2. Построение эпюр внутренних усилий в многопролетных шарнирных балках

Внешняя нагрузка на балки обычно такова, что продольные силы в них не возникают. Таким образом, для балок строятся только две эпюры: изгибающего момента M и поперечной силы Q.

Многопролетная балка расчленяется по шарнирам на отдельные звенья. Каждое звено оказывается однопролетной статически определимой балкой. Звенья рассчитываются в последовательности, определяемой с помощью этажной схемы. Для этого звенья нумеруются следующим образом. Цифрой 1 обозначаются звенья, на которые не опираются другие звенья, цифрой 2 – звенья, на которые опираются звенья 1 и т.д. Расчет начинается со звеньев номер 1. Здесь определяются опорные реакции и строятся эпюры M и Q. Затем рассматриваются звенья под номером 2. На каждое из них действует помимо внешней нагрузки давление соседнего звена 1, численно равное опорной реакции этого звена и направленное в противоположную сторону. Звенья под номером 3 рассчитываются на действие внешней нагрузки и давление примыкающего звена 2. Таким образом, в первую очередь рассчитываются звенья, находящиеся на самом верху этажной схемы, а в последнюю - звенья нижнего этажа.

Покажем последовательность расчета на примере балки, изображенной на рис.3.4,а. В начале расчета строится этажная схема балки и нумеруются ее звенья (рис. 3.4,б). Схема взаимодействия звеньев балки показана на рис. 3.4,в.

Опишем кратко построение эпюр на звеньях балки. Предварительно заметим следующее: в курсе сопротивления материалов, как и в примерах раздела 2.3 на участках балок определялись аналитические функции . А эпюры изображались как графики этих функций. В курсе строительной механики в силу сложной геометрии исследуемых стержневых систем получение аналитических функций нецелесообразно и поэтому эпюры усилий строятся на основе их свойств, определенных в разделе 2.4.

При расчете звена DE, которое имеет номер 1, опорные реакции можно не находить. Определяем момент на консоли по определению раздела 2.1:

т.е. в любом сечении момент равен 100 и растянуты верхние волокна. Пролет балки загружен равномерно распределенной нагрузкой. Здесь строим эпюры по правилам раздела 2.5. Моменты в крайних сечениях известны: 0 (т.D) и –100 (т.E). Соединяем ординаты пунктирной прямой. Ордината в середине пролета равна –50 (рис. 3.5). От этой точки в направлении действия нагрузки откладываем величину: . Окончательно, ордината в центральном сечении равна +43,75.

Рис. 3.5.

Для построения эпюры Q в пролете определяем по формуле (2.3) ординаты в крайних точках пролета:

На консоли Q=0. По эпюре Q находим:

.

Звено 2 (BCD) находится под действием заданной нагрузки и силы со стороны звена 1 (рис. 3.6,а).

Для построения эпюр достаточно найти только реакцию

Далее определяем моменты в сечении 1 и в сечении над опорой С (рис. 3.6,б). Откладываем соответствующие ординаты на растянутых волокнах. Строим два линейных участка эпюры M в пролете: от нуля в шарнире B до ординаты 40 в сеч. 1 и от 40 до –170 в сечении С. На консоли центральную ординату параболы определяем по формуле (2.4):

Ординаты эпюры Q в пролете вычисляются по определениям раздела 2.1 (рис.3.6,в). На консоли ординаты Q находятся по формуле (2.3):

.

Звено 3 (AB) находится под действием равномерно распределенной нагрузки и реакции . Здесь эпюры M и Q (рис. 3.7) могут быть построены или суммированием эпюр задач, представленных на рис. 2.14,а,б, или по правилам раздела 2.5.

Рис. 3.7.

Эпюры M и Q в исходной шарнирной балке, построенные по звеньям от общей оси, представлены на рис. 3.8.