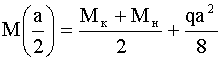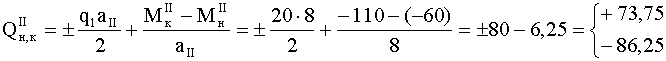|
 |
 |
 |
|
2.3. Построение эпюр усилий в простых балках
|
Продемонстрируем применение изложенных выше правил на простых примерах.
З а д а ч а 1. Построить эпюры усилий в шарнирно-опертой балке, загруженной в центральном сечении силой P (рис. 2.7).
Статический расчет начнем с определения опорных реакций. Балка опирается на три связи, не параллельные и не пересекающиеся в одной точке. Это минимальное количество связей, которое обеспечивает и статическую определимость и геометрическую неизменяемость системы. Зададим произвольные направления составляющих опорных реакций:
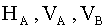 . .
Составим три уравнения равновесия для всей системы:


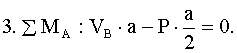
Из третьего и второго уравнений определяем:

Рис. 2.8.
Для построения эпюр выделим на балке два участка: I и II, разделенных точкой приложения силы P. Наметим на каждом участке сечение с текущей координатой x. Вычислим в нем усилия M и Q по правилам, приведенным в начале раздела 2 (рис.2.8).
Направление вектора
 определяется из того условия, что выделенная часть балки должна находиться в равновесии. В частности, момент внешних и внутренних усилий относительно центра тяжести сечения x должен быть равен нулю. Момент внешней силы определяется из того условия, что выделенная часть балки должна находиться в равновесии. В частности, момент внешних и внутренних усилий относительно центра тяжести сечения x должен быть равен нулю. Момент внешней силы
 в сечении x действует по часовой стрелке. Внутренний момент, уравновешивая его, действует в противоположном направлении. Таким образом, в каждом сечении x растянуты нижние волокна, со стороны которых откладываются ординаты линейной эпюры I участка. в сечении x действует по часовой стрелке. Внутренний момент, уравновешивая его, действует в противоположном направлении. Таким образом, в каждом сечении x растянуты нижние волокна, со стороны которых откладываются ординаты линейной эпюры I участка.
На II участке из двух внешних сил
 и и
 больший момент в любом сечении создает сила больший момент в любом сечении создает сила
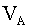 . Внутренний момент . Внутренний момент
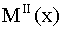 направлен так, чтобы компенсировать момент внешних сил в сечении x. Он растягивает нижние волокна. На них строится линейная эпюра M II участка. направлен так, чтобы компенсировать момент внешних сил в сечении x. Он растягивает нижние волокна. На них строится линейная эпюра M II участка.
Отметим пунктиром нижние волокна балки. Ординаты построенной эпюры M находятся со стороны тех же волокон, что и пунктир, следовательно, они положительны.
Перейдем к построению эпюры Q. Величины перерезывающих сил на обоих участках балки одинаковы и равны по
 /2. На участке I ординаты эпюры Q положительны, так как при движении по балке в положительном направлении оси x (слева направо) растут положительные ординаты эпюры M и /2. На участке I ординаты эпюры Q положительны, так как при движении по балке в положительном направлении оси x (слева направо) растут положительные ординаты эпюры M и
 на участке. На II участке положительные ординаты эпюры M уменьшаются, здесь на участке. На II участке положительные ординаты эпюры M уменьшаются, здесь
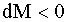 и эпюра Q отрицательна. и эпюра Q отрицательна.
Эпюра продольных усилий не строится, так как значение N в любом сечении равно нулю.
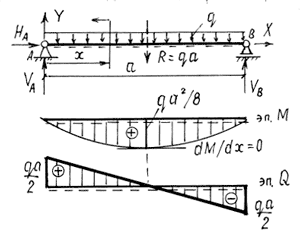
Задача 2. Шарнирно-опертая балка под действием равномерно распределенной нагрузки (рис. 2.9).
Определение опорных реакций (порядок уравнений равновесия изменен для удобства.)
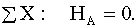

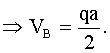
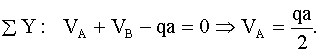

Рассмотрим часть балки по левую сторону от сечения с координатой x (рис. 2.10):
Рис. 2.10.
На базе правил вычисления усилий (см. раздел 2.1) запишем функции, определяющие внутренние усилия в сечении x :
В любом сечении x балки внутренний момент
 направлен против часовой стрелки. Он уравновешивает результирующий момент внешних сил направлен против часовой стрелки. Он уравновешивает результирующий момент внешних сил
 и и
 , который направлен по часовой стрелке, так как преобладающим в любом сечении является момент силы , который направлен по часовой стрелке, так как преобладающим в любом сечении является момент силы
 . Заметим, что функция . Заметим, что функция
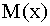 является квадратичной параболой. В общем случае функция записывается выражением является квадратичной параболой. В общем случае функция записывается выражением
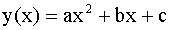 . Три коэффициента определяют вид параболы. Следовательно, для построения графика функции достаточно определить ординаты трех точек, через которые проходит парабола. Для построения эпюры . Три коэффициента определяют вид параболы. Следовательно, для построения графика функции достаточно определить ординаты трех точек, через которые проходит парабола. Для построения эпюры
 в рассматриваемом случае имеем: в рассматриваемом случае имеем:
Через три ординаты: 0,
 , 0 проводится на растянутых нижних волокнах квадратичная парабола, т.е. график функции , 0 проводится на растянутых нижних волокнах квадратичная парабола, т.е. график функции
 . Проведем пунктир на нижних волокнах балки. Тогда ординаты эпюры M оказываются положительными. . Проведем пунктир на нижних волокнах балки. Тогда ординаты эпюры M оказываются положительными.
Функция
 изменяется по длине балки по линейному закону. Для построения линейной эпюры вычислим величины перерезывающих сил и определим знаки (рис. 2.11) соответствующих ординат в двух крайних сечениях: изменяется по длине балки по линейному закону. Для построения линейной эпюры вычислим величины перерезывающих сил и определим знаки (рис. 2.11) соответствующих ординат в двух крайних сечениях:
Рис. 2.11.
Отложив
 и и
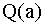 с учетом знака, соединяем их прямой линией. Обратим внимание на то, что в точке, где с учетом знака, соединяем их прямой линией. Обратим внимание на то, что в точке, где

 ордината эпюры моментов имеет экстремальное значение, согласно зависимости (2.1). ордината эпюры моментов имеет экстремальное значение, согласно зависимости (2.1).
Задача 3. Шарнирно-опертая балка, загруженная в центральном сечении сосредоточенным моментом (рис. 2.12).
Определение опорных реакций:
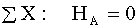 . .
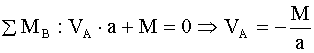 . .

 . .
Изменяем направление вектора
 на противоположное, так как исходное направление не отвечает условиям равновесия на противоположное, так как исходное направление не отвечает условиям равновесия
Заметим, что перед построением эпюр направление векторов реакций всегда должно соответствовать положительному значению реакций. Иначе невозможно правильно определить направление изгибающих моментов и продольных сил в сечениях.
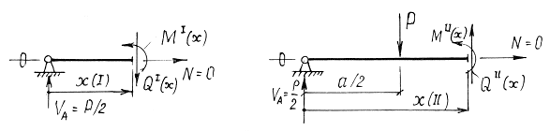
Найдем внутренние усилия на I участке в сечении с координатой x, отсчитываемой от левого конца балки и на II участке в сечении с координатой
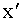 , отсчитываемой от правого конца (рис. 2.13). , отсчитываемой от правого конца (рис. 2.13).
Рис. 2.13.
Получаем, что на I участке эпюра M изменяется по линейному закону от значения 0
 до значения до значения
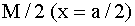 . Ординаты эпюры M откладываются со стороны верхних, растянутых волокон. На II участке картина аналогичная, но растянуты нижние волокна. . Ординаты эпюры M откладываются со стороны верхних, растянутых волокон. На II участке картина аналогичная, но растянуты нижние волокна.
Ординаты эпюры Q постоянны на обоих участках и равны
 . Их знак – отрицательный, так как при движении по оси балки слева направо (в положительном направлении оси . Их знак – отрицательный, так как при движении по оси балки слева направо (в положительном направлении оси
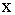 ) ординаты эпюры M убывают и ) ординаты эпюры M убывают и
 . .
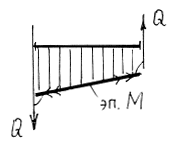
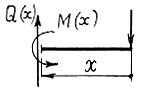
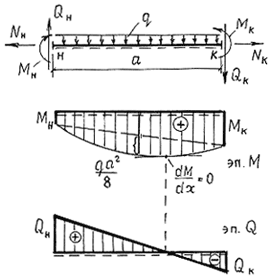
Рассмотрим, но не так подробно, примеры построения эпюр усилий в консольных балках (рис. 2.14, а-в).
Во всех случаях нагружения для построения эпюр M и Q
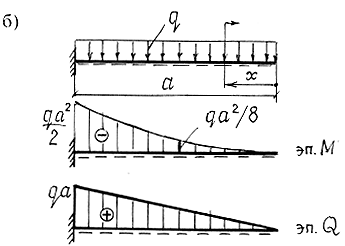
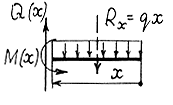
 опорные реакции можно не искать. Для определения величин внутренних усилий достаточно знать внешние усилия, действующие по одну сторону от сечения. На рис.2.14 приведены формулы для вычисления внутренних усилий в сечениях с координатой x, отсчитываемой от правого конца балок. Придавая x конкретные значения на промежутке опорные реакции можно не искать. Для определения величин внутренних усилий достаточно знать внешние усилия, действующие по одну сторону от сечения. На рис.2.14 приведены формулы для вычисления внутренних усилий в сечениях с координатой x, отсчитываемой от правого конца балок. Придавая x конкретные значения на промежутке
 , строим эпюры усилий. Отметим, что для построения линейной эпюры нужно знать ординаты в двух сечениях балки, для построения квадратичной параболы – в трех. , строим эпюры усилий. Отметим, что для построения линейной эпюры нужно знать ординаты в двух сечениях балки, для построения квадратичной параболы – в трех.
Рис. 2.14.
|






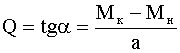


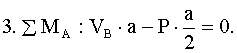




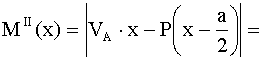

 ;
; 

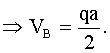
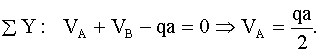



 ,
,


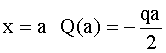


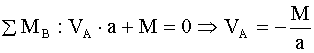 .
.
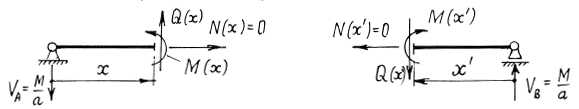
 ,
,
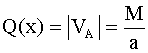 ,
,
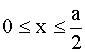 .
.
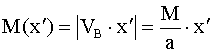 ,
,
 ,
,
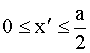




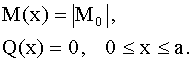



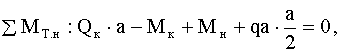
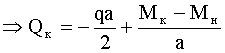 .
. 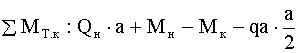
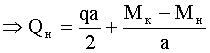

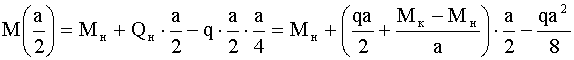 ,
,