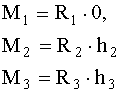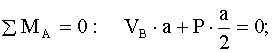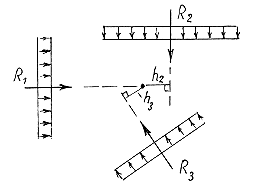
Расчетные схемы сооружений. Понятие статической определимости стержневой системы.

1.1. Расчетные схемы сооружений.

В строительной механике каждая стержневая система изображается не реальной конструкцией, а расчетной схемой. На ней должны быть показаны: оси стержней, их соединения друг с другом, опорные закрепления, нагрузки. Выбор расчетной схемы сооружения является одним из сложнейших элементов расчета. Этот вопрос рассмотрен во многих работах, например [2].В данной работе мы исследуем уже готовые схемы сооружений.

Будем считать, что в расчетной схеме стержни могут иметь между собой и с неподвижным основанием два вида соединений: жесткое и шарнирное. Жесткое соединение называется жестким узлом. Жесткие узлы (рис. 1.1) обеспечивают одинаковость линейных и угловых перемещений концов стержней, т.е. жесткие узлы не допускают относительного поворота стержней в них сходящихся. Шарнирные узлы (рис.1.1) обеспечивают одинаковость только линейных перемещений концов соединяемых стержней. В шарнирном узле концы стержней, сходящихся в идеальном шарнире, могут свободно, без трения, поворачиваются относительно друг друга.

Опорные закрепления плоских стержневых систем, загруженных силами, лежащими в их плоскости, чаще всего бывают трех основных типов:

шарнирная подвижная опора, эквивалентная одному опорному стержню (рис. 1.2,а). Она не допускает перемещений, перпендикулярных плоскости качения. Линия действия опорной реакции проходит через центр опорного шарнира и перпендикулярна плоскости качения;

шарнирная неподвижная опора, эквивалентная двум опорным стержням, пересекающимся в опорном шарнире (рис. 1.2,б). Опора не допускает линейных перемещений. Линия действия опорной реакции проходит через центр опорного шарнира. Определению подлежат две составляющие опорной реакции;

защемляющая опора, эквивалентная трем опорным стержням, не пересекающимся в одной точке (рис. 1.2,в). Препятствует линейным и угловым перемещениям опорного узла. Определить нужно три неизвестные: две составляющие опорной реакции и опорный момент.

Также часто встречается защемляющая подвижная опора или скользящая заделка (рис. 1.3). Она допускает линейное перемещение в каком-то одном направлении. Опора эквивалентна двум опорным связям, направленным перпендикулярно линии качения и вызывает две составляющие опорной реакции: момент и силу, перпендикулярную линии качения.

В качестве нагрузок на исследуемые стержневые системы будем рассматривать следующие:

• равномерно-распределенная по длине стержня нагрузка размерностью [кН/м];
• сосредоточенная сила размерностью [кН];
• сосредоточенный изгибающий момент размерностью [кНм].

Приведем примеры расчетных схем указанных выше четырех основных типов плоских стержневых систем:

1.2. Условие статической определимости стержневой системы

Методы расчета статически определимых и статически неопределимых систем различны. В связи с этим сразу после составления расчетной схемы сооружения необходимо определить является ли данная система статически определимой или нет.

Когда плоская стержневая система загружена силами, лежащими в ее плоскости, внешние нагрузки и опорные реакции должны удовлетворять трем уравнениям равновесия. Ими могут быть, например, следующие: равенство нулю суммы проекций всех сил на две взаимно перпендикулярные оси и равенство нулю суммы статических моментов относительно любой точки плоскости. Напомним: статический момент силы относительно некоторой точки определяется как произведение силы на плечо. Плечо силы есть расстояние от точки, в которой вычисляется момент, до линии действия силы (рис. 1.4).

В случае равномерно-распределенной нагрузки статический момент определяется как момент силы, являющейся равнодействующей распределенной нагрузки (рис. 1.5).

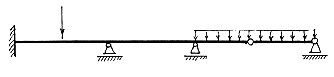
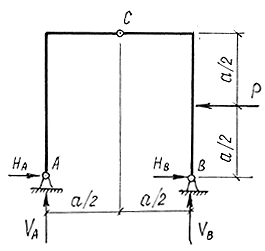
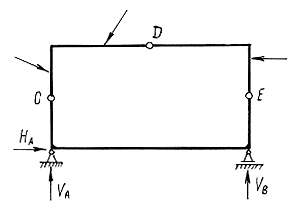
Как уже указывалось, статически определимые системы могут быть рассчитаны с использованием только уравнений равновесия.

Рассмотрим раму, изображенную на рис.1.6.

Здесь левая опора А – шарнирная неподвижная. Опорная реакция имеет две составляющие на оси OX и OY: и .

Правая опора В – шарнирная подвижная. Опорная реакция одна - . Направление опорных реакций выбрано произвольно.

Три составляющие опорных реакций могут быть найдены из трех уравнений равновесия:

1. Сумма проекций всех сил на горизонтальную ось: 2. Сумма проекций всех сил на вертикальную ось: 3. Сумма статических моментов всех сил относительно точки А:

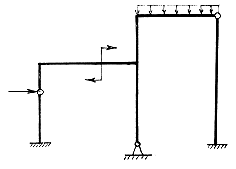
При записи моментного уравнения составляется алгебраическая сумма статических моментов: моменты, вращающие в одном направлении, имеют один знак; моменты, вращающие в другом направлении – другой знак.

Рассмотрим еще один пример (рис. 1.7). Здесь обе опоры шарнирные неподвижные. Определению подлежат четыре составляющие опорных реакций: .
Для их нахождения имеются только три уравнения равновесия. Одну из составляющих не найти, следовательно, задача один раз статически неопределима.

Рис. 1.7.

Рис. 1.8.

Изменим расчетную схему, поставив шарнир С (рис. 1.8). Появляется дополнительное уравнение: равенство нулю момента в шарнире С. Для нахождения четырех составляющих опорных реакций теперь имеем четыре уравнения равновесия:

Из этого примера видно, что шарнир, соединяющий два стержня или вообще два жестких элемента:

понижает степень статической неопределимости на единицу. Но шарнир может соединять и три стержня или три жестких элемента:

Его можно представить как два одиночных шарнира, слившиеся в один. Такой шарнир называется двойным. Он понижает степень статической неопределимости на две единицы. Можно ввести понятие кратности шарнира. Она равна числу дополнительных уравнений равновесия, которые дает данный шарнир. Кратность шарнира может быть вычислена по формуле: число стержней, соединяемых шарниром минус единица. Например, кратность следующего шарнира равна трем:

Для полной статической определимости рама должна быть статически определима как относительно опорных реакций (так называемая внешняя статическая определимость), так и относительно усилий в ее элементах (внутренняя статическая определимость).

Рассмотрим раму, изображенную на рис. 1.6. Выше было показано, что данная система внешне статически определима. Проведем сечение, разделяющее раму на две части (рис. 1.9). Заменим действие отброшенных частей равнодействующими внутренних усилий. В плоских системах внутренние усилия имеют три составляющие:

Усилия M,Q,N, действующие на левую и правую части, равны и противоположно направлены в силу равенства действия и противодействия. В строительной механике для векторов внутренних усилий не вводятся правила знаков, связанные с системой осей координат. На рис. 1.9 показаны произвольные направления усилий. О правилах знаков будет сказано ниже (см. раздел 2.2.).

Каждая из частей рамы должна находиться в равновесии под действием приложенных к ней известных внешних сил и неизвестных внутренних усилий M,Q,N. Эти три величины можно найти из трех уравнений равновесия для одной из частей рамы.

Для левой части рамы имеем:

Уравнения равновесия для другой части рамы при найденных значениях M,Q,N должны удовлетворяться тождественно. Следовательно, рассмотренная рама внешне и внутренне статически определима.

Исследуем теперь раму, представляющую собой замкнутый контур (рис. 1.10).Внешне она статически определима, но внутренне статически неопределима. Действительно, в ней нельзя провести сечение, разделяющее ее на две самостоятельные не связанные между собой части и в то же время пересекающее только один стержень. Каждое сечение пересекает два стержня, для определения шести усилий в которых имеются только три уравнения равновесия. Поэтому замкнутый контур трижды статически неопределим. Но если в замкнутом контуре поставить три одиночных шарнира (рис. 1.11), то это даст три недостающих уравнения, и система превратиться в статически определимую.

Рис. 1.10.

Рис. 1.11.

Из всего сказанного легко заключить, что степень статической неопределимости рамы можно вычислить по следующей формуле

(1.1)

где - степень статической неопределимости, - число составляющих опорных реакций, - число замкнутых контуров, 3 – число уравнений равновесия - число одиночных шарниров (или суммарная кратность всех шарниров за исключением опорных).

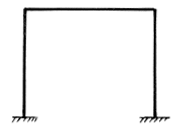
Если для исследуемой стержневой системы оказалось:

1) = 0, то система статически определима;
2) > 0, то система статически неопределима;
3) < 0, то система геометрически изменяема.

К геометрически изменяемым относят такие системы, которые могут перемещаться без деформации. Геометрически неизменяемыми считаются системы, перемещения в которых возникают только в результате деформации. Для исследования геометрической неизменяемости стержневой системы можно положить все стержни системы абсолютно жесткими, тогда они станут недеформируемыми. Если в полученной недеформируемой системе возможны перемещения, то система – геометрически изменяемая, а если перемещения невозможны, то система – геометрически неизменяемая.

Рассмотрим простые примеры. Рама, изображенная на рис. 1.12, имеет жесткие узлы и неподвижные опоры. При условии абсолютной жесткости стержней точки рамы не могут перемещаться при любых нагружениях. Следовательно, данная рама является геометрически неизменяемой.

Рис. 1.12.

Рис. 1.13.

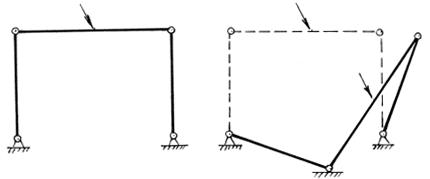
Система с шарнирными узлами и шарнирными опорами, изображенная на рис.1.13, подобна механизму ( = -1). При нагрузке, имеющей горизонтальную составляющую, она начнет движение и будет продолжать его до тех пор, пока не встретит какое-нибудь препятствие, т.е. не получит дополнительные опорные связи. При отсутствии дополнительных опорных связей движение системы будет продолжаться вплоть до получения ею, если это возможно, положения, соответствующего состоянию равновесия (рис. 1.13). Таким образом, стержневая система на рис. 1.13 является геометрически изменяемой.

Геометрически изменяемые системы не могут нести произвольную нагрузку, так как это приводит или к изменению их формы (например, падение отдельных частей или всей системы) или к возникновению в элементах системы бесконечно больших усилий, которые также приводят к разрушению стержневой системы. Подобные ситуации возникают, когда стержневая конструкция не имеет достаточного количества опорных связей или имеет избыточное число шарниров. Возможны также случаи неверной расстановки шарниров или опорных связей и тогда геометрически изменяемой оказывается статически определимая или даже статически неопределимая система.

Вопрос о геометрической неизменяемости конструкции можно решить на основе структурного анализа стержневой системы [3]. Эти проблемы выходят за рамки данной работы, здесь рассматриваются только вопросы исследования геометрической изменяемости шарнирных балок и ферм (см. разделы 3.1 и 5.2).