| |
Санкт-Петербургский Государственный Политехнический Университет |
| КАФЕДРА СТРОИТЕЛЬНОЙ МЕХАНИКИ И ТЕОРИИ УПРУГОСТИ | |
| |
Для получения задания выберите название задания и выданный Вам преподавателем номер варианта, после чего нажмите кнопку "Готово":
| Вариант: |
|
ЧАСТЬ1: ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
Задание 1. Решение систем линейных алгебраических уравнений
Дана система:
1. Записать систему в матричной форме.
2. Найти решение системы методом Гаусса.
3. Проверить правильность решения и определить вектор невязок (погрешностей).
4. Исследовать устойчивость решения системы и сделать вывод о степени её обусловленности.
Задание 2. Математическая обработка результатов эксперимента
В результате эксперимента получена серия значений X иY:
1. По результатам эксперимента проанализировать различные варианты зависимости Y=F(X), построенные методами средней, наименьших квадратов, Лагранжа, кубических сплайнов.
2. Из всех имеющихся вариантов выбрать, на Ваш взгляд, наиболее подходящий для данного случая метод интерполяции , записать для него аналитическое выражение функции Y=F(X) и построить её график.
Задание 3. Численное интегрирование.
Дан интеграл:
1. Найти приближенные значения интеграла на сетках из 2, 4, 8 и 16 участков с использованием формул прямоугольников, трапеций, Симпсона.
2. Найти аналитическое решение задачи и для полученных приближённых решений определить абсолютные и относительные погрешности. Результаты удобно оформить в виде таблицы:
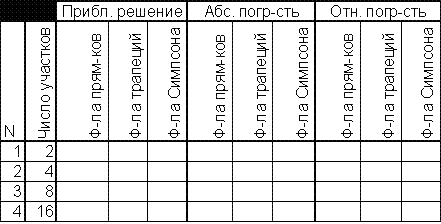
3. Найти (вручную) приближённое решение по формуле Симпсона на сетке из 1 участка.
4. Сделать выводы о точности различных методов численного интегрирования.
Задание 4. Численное решение уравнений вида f(x)=0.
Дано уравнение:
.
1. Записать уравнение в виде f(x)=0, построить график функции f(x), определить по графику количество корней уравнения.
2. Определить интервал изоляции корня (если корней несколько, то для любого из них по Вашему выбору).
3. Найти корни уравнения с использованием методов половинного деления, хорд и Ньютона.
4. Сделать выводы о точности и скорости сходимости решения для этих методов (по количеству итераций, требуемых для получения решения с точностью до восьми знаков после запятой).
Желаем Вам приятной работы и хороших файлов !
| Вариант: |
|
ЧАСТЬ2: ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ
Задание 1. Метод Эйлера.
Дифференциальное уравнение y ' (x)=f(x,y) определено в пределах интервала с границами a и b, где:
Граничное условие:
1. Найти решение данной задачи Коши методом Эйлера на сетках из 2, 4, 8, 16 и 32 участков.
2. Построить графики полученных решений.
3. Найти аналитическое решение задачи.
4. Для точки x=b найти абсолютные и относительные погрешности приближенных решений, оценить порядок сходимости метода. Результаты удобно оформить в виде таблицы:
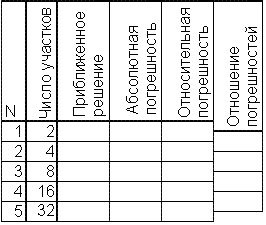
5. Сделать выводы о точности метода Эйлера.
Задание 2. Метод Рунге-Кутта.
1. Найти решение задачи Коши из предыдущего задания методом Рунге-Кутта на сетках из 2,4,8,16 и 32 участков.
2. Построить графики полученных решений.
3. Для точки x=b найти абсолютные и относительные погрешности приближенных решений, оценить порядок сходимости метода.
4. Сделать выводы о точности метода Рунге-Кутта в сопоставлении с методом Эйлера.
Задание 3. Метод Шварцмана.
1. Уточнить методом Шварцмана решения задачи из задания №1, полученные методом Эйлера на первых трех сетках для точки x=b.
2. Найти абсолютную и относительную погрешности уточненного решения.
3. Сделать выводы об эффективности метода Шварцмана.
Задание 4. Решение систем дифференциальных уравнений.
Система дифференциальных уравнений Лотки-Вольтерра, описывающая динамику числа особей в популяциях жертв x(t) и хищников y(t), имеет вид:
.
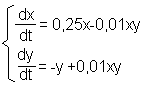1.Найти решение данной задачи для временного интервала 40 лет на сетках из 20 и 40 участков методом Рунге-Кутта при начальных условиях x(t)=80, y(t)=20.
2. Построить графики полученных решений x(t), y(t), а также график зависимости y(x).
3. Сделать выводы о качестве полученных решений и модели Лотки-Вольтерра.
Задание 5. Решение дифференциального уравнения второго порядка.
Необходимо найти прогиб свободного конца балки, изображенной на рисунке:
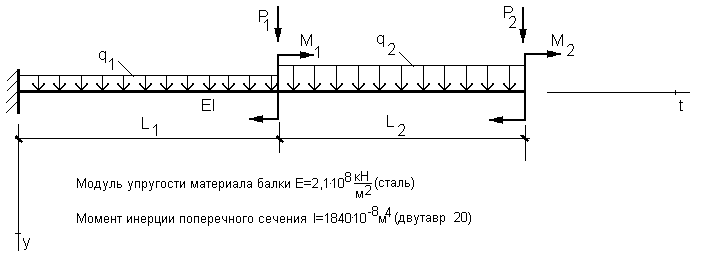
Дифференциальное уравнение изгиба балки имеет вид:
,
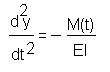где M(t) -выражение для изгибающего момента.
1. Численное решение задачи найти методом Рунге-Кутта на сетках из 10 и 20 участков.
2. Построить график изогнутой оси балки (ось прогибов направить вниз).
3. Пользуясь табличными решениями , на основе принципа суперпозиций найти точное решение задачи.
4. Найти абсолютные и относительные погрешности численных решений.
5. Сделать выводы о точности численных решений.
Задание 6. Исследование устойчивости решения задачи Коши и неявная схема метода Эйлера.
Дана задача:
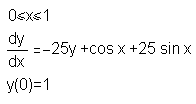
1. Найти решения данной задачи методом Эйлера и по неявной схеме метода Эйлера на сетках из 2, 4, 8, 16 и 32 участков.
2. Построить графики полученных решений.
3. Сопоставить полученные приближенные решения с известным точным решением:
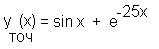
4. Сделать выводы оточности и устойчивости решений, полученных методом Эйлера и по неявной схеме метода Эйлера.
Задание 7. Практическая задача.
ЗАДАЧА ОБ ИСТЕЧЕНИИ ЖИДКОСТИ ИЗ ЦИЛИНДРИЧЕСКОГО РЕЗЕРВУАРА
Расходом Q (куб.м/сек) называется объем воды, проходящий через отверстие или трубу в единицу времени.
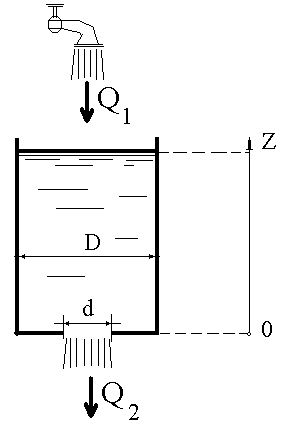
В цилиндрический резервуар диаметром D=10 м поступает расход Q1=2 куб.м./сек. и через отверстие уходит расход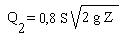 
, где S - площадь отверстия диаметром d=0,5 м, g= 9,81 м/с2 , Z(t) - глубина воды в резервуаре, удовлетворяющая уравнению:
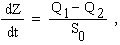
причем S0 - площадь свободной поверхности жидкости.
Необходимо при начальном условии Z=20 м при t=0 определить уровень жидкости через промежуток времени t=3 мин (180 сек).
ЗАДАЧА О БОЕВЫХ ДЕЙСТВИЯХ
Одна из противоборствующих армий x и y обладает численным преимуществом, другая - более совершенным оружием. Численный состав армий в момент времени t определяется уравнениями:
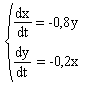
и перед началом сражения составлял x = 50 тыс. чел. у = 30 тыс. чел.
Сражение ведется до полного уничтожения одной из сторон.
Кто, х или у победит в сражении?
ЗАДАЧА О РАСПРОСТРАНЕНИИ НОВОСТЕЙ
В городе живет N= 6 млн. жителей. В 8 часов утра 1/100 часть жителей города узнала по радио столичную новость, после чего радиопередатчик вышел из строя. В дальнейшем эта новость распространялась посредством общения людей друг с другом. Число жителей x(t), узнавших новость к моменту времени t, определяется уравнением:
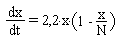
К какому моменту времени новость узнает половина жителей города ?
KРИМИНАЛЬНАЯ ЗАДАЧА
При обнаружении трупа его температура составляла х=31 градус. Считая, что в момент убийства температура тела составляла х=36,6 градусов, а зависимость температуры х от времени t определяется уравнением:
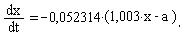
где а - температура наружного воздуха, необходимо определить, сколько времени прошло с момента убийства, если а= 15 градусов. (Время измеряется в минутах.)
ЗАДАЧА О РАСПРОСТРАНЕНИИ СЛУХОВ
В городе живет N= 5 млн. жителей. 10 ноября один из них стал распростронять слух о "важном событии". В дальнейшем эта "информация" распространялась посредством общения людей друг с другом. Число жителей x, узнавших новость к моменту времени t, определяется уравнением:
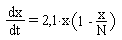
К какому моменту времени 1 млн. жителей города будет "осведомлен" о важном событии?
КРИМИНАЛЬНАЯ ЗАДАЧА
Если при обнаружении трупа измерить его температуру, то предполагая, что в момент убийства температура тела составляла 37 градусов, можно определить время, прошедшее с момента убийства, при условии, что труп не остыл до температуры окружающего воздуха. Температура тела определяется уравнением:
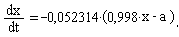
где а - температура окружающего воздуха. Пусть а=23 градуса. Необходимо определить время остывания тела до температуры окружающего воздуха. (Время измеряется в минутах.)
ЗАДАЧА О ТЛЕ
Число особей x(t) в популяции яблоневой тли в момент времени t определяется уравнением:
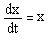
10 августа, когда начались наблюдения, было х=1000. Сколько особей будет 20 августа?
ЗАДАЧА О ВОДОПРИНИМАЮЩЕМ КОЛОДЦЕ
Квадраты глубин кривой депрессии для круглого колодца удовлетворяют уравнению:
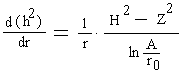
где r0=5м, Н=4м, z=8м, А=1000, а=1м (см.обозначения на рисунке).
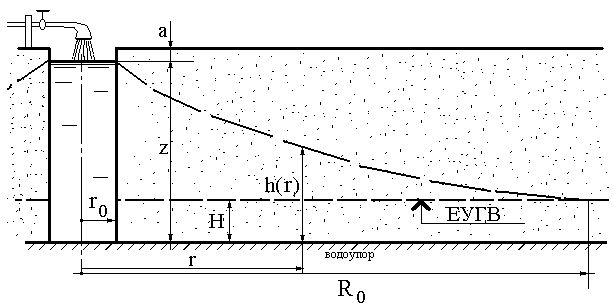
Необходимо определить pадиус влияния колодца R0 (ЕУГВ - Естественный Уровень Урунтовых Вод).
ЗАДАЧА ОБ ИСТЕЧЕНИИ ЖИДКОСТИ ИЗ СФЕРИЧЕСКОГО РЕЗЕРВУАРА
Расходом Q (куб.м/сек) называется объем воды, проходящий через отверстие или трубу в единицу времени.
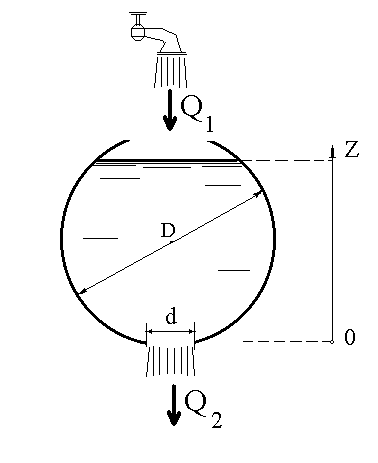
В сферический резервуар диаметром D=8 м поступает расход Q1=4,1 куб.м./сек. и через отверстие уходит расход 
, где S - площадь отверстия диаметром d=1 м, g= 9,81 м/с2 , Z(t) - глубина воды в резервуаре, удовлетворяющая уравнению:
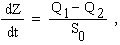
причем S0 - площадь свободной поверхности жидкости.
Необходимо при начальном условии Z=7 м при t=0 определить уровень жидкости через промежуток времени t=4 мин (240 сек).
ЗАДАЧА О ПОЛЕТЕ МЕТЕОРОЛОГИЧЕСКОЙ РАКЕТЫ
Запас топлива в ракете для метеоролгических измерений в верхних слоях тропосферы рассчитан на 30 сек. работы двигателя. Масса ракеты во время полета меняется по закону m(t)=M-qt , где M = 2000 кг -стартовая масса полностью заправленной топливом ракеты, q = 50 кг/сек -расход топлива, t -время, прошедшее с момента старта. Высота подъема ракеты определяется уравнением:
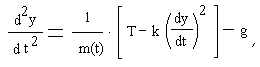
где Т = 100000кН - тяговое усилие двигателя, k = 0,3 - коэффициент, учитывающий сопротивление воздуха, g = 9,81 м/с2 - ускорение свободного падения.
На какую высоту поднимется ракета к моменту, когда закончится топливо?
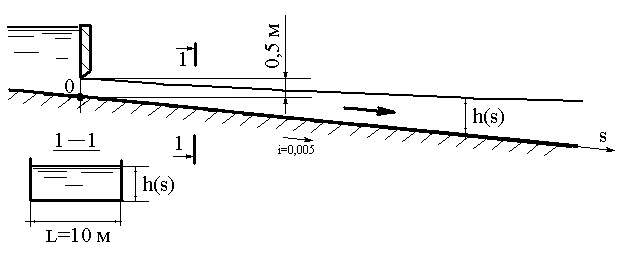
ЗАДАЧА ПОСТРОЕНИЯ КРИВОЙ СВОБОДНОЙ ПОВЕРХНОСТИ ЖИДКОСТИ
Длинный канал прямоугольного поперечного сечения шириной l = 10 м, продольным уклоном дна i = 0,005 перегорожен щитом, приподнятым над дном на высоту 0,5 м.
Глубина воды в канале определяется уравнением:
,
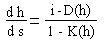где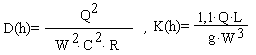 
, причем s -ось, направленная в сторону движения жидкости, Q = 20 куб.м./сек -расход воды, идущей по каналу, 
-площадь поперечного сечения потока, g = 9,81 м/с2 -ускорение свободного падения,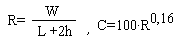 
-гидравлические коэффициенты.
Каков будет уровень жидкости в канале в 200 м ниже по течению от щита ?
ХИМИЧЕСКАЯ ЗАДАЧА
Объем вещества x(t), образовавшегося в результате химической реакции к моменту времени t , определяется уравнением:
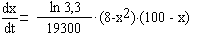
Через 20 минут после начала реакции объем вещества составлял x= 13 литров.
Необходимо определить, cколько образовалось вещества через 10 минут после начала эксперимента.
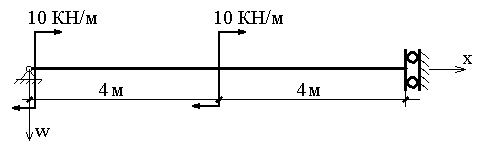
ЗАДАЧА ОБ ИЗГИБЕ КОНСОЛЬНОЙ БАЛКИ
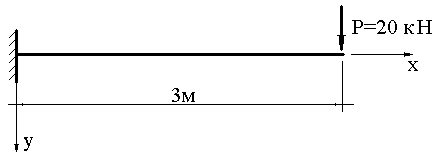
Консольная балка длиной 3 м подвержена действию сосредоточенной силы величиной Р=20кН, приложенной на ее конце. Необходимо построить изогнутую ось балки и найти ее максимальный прогиб, если дифференциальное уравнение, описывающее изгиб балки, выглядит следующим образом:
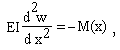
где M(x) - закон изменения изгибающего момента, Е=210 000 000 кН/кв.м. - модуль упругости стали, I=0,00001290 м4 (двутавр N 18) -момент инерции поперечного сечения балки.
ЗАДАЧА ОБ ОСАДЕ ГОРОДА
Численный состав армии, осаждающей город x(t) и обороняющей город y(t)определяется системой уравнений:
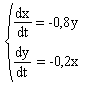
В начале осады было x = 50 тыс. чел. у = 30 тыс.чел. Осада продолжается до полного уничтожения одной из сторон.
Сколько будет продолжаться осада (время измеряется в сутках)?
ЗАДАЧА О ВОДООТДАЮЩЕМ КОЛОДЦЕ
Квадраты глубин кривой депрессии для круглого колодца удовлетворяют уравнению:
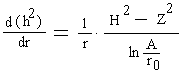
где r0=5м, Н=8м, z=4м, А=800, а=1м (см.обозначения на рисунке).
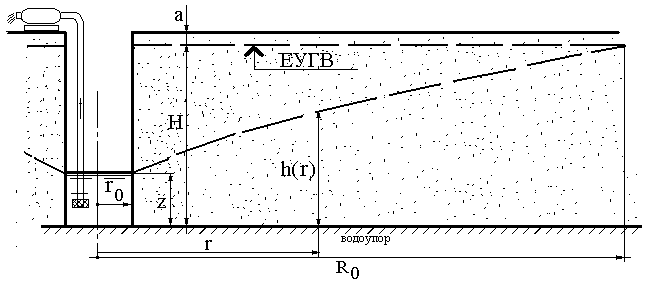
Необходимо определить pадиус влияния колодца R0 (ЕУГВ - Естественный Уровень Урунтовых Вод).
ЗАДАЧА ОБ ИЗГИБЕ КОНСОЛЬНОЙ БАЛКИ
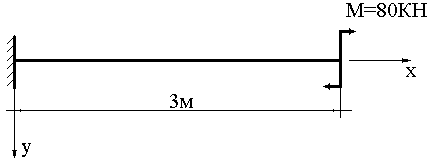
Консольная балка длиной 3 м подвержена действию сосредоточенного момента величиной М=80 КНм, приложенного на ее конце.Необходимо построить изогнутую ось балки и найти ее максимальный прогиб, если дифференциальное уравнение, описывающее изгиб балки, выглядит следующим образом:
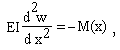
где M(x) - закон изменения изгибающего момента, Е=210 000 000 кН/кв.м. - модуль упругости стали, I=0,00001290 м4 (двутавр N 18) -момент инерции поперечного сечения балки.
ЗАДАЧА О ПАДЕНИИ ГРУЗА
С вертолета, находящегося на высоте Н над землей сбрасывают груз массой m = 250 кг. Движение груза описывается уравнением:
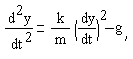
где k=0,3 - коэффициент, учитывающий сопротивление воздуха, g = 9,81 м/с2 - ускорение свободного падения, у(t) - высота груза над поверхностью земли в момент времени t. Необходимо определить время падения груза, если H = 1000м.
ЗАДАЧА ОБ ИСТЕЧЕНИИ ЖИДКОСТИ ИЗ ЦИЛИНДРИЧЕСКОГО РЕЗЕРВУАРА
Расходом Q (куб.м/сек) называется объем воды, проходящий через отверстие или трубу в единицу времени.
В цилиндрический резервуар диаметром D=10 м поступает расход Q1=2 куб.м./сек. и через отверстие уходит расход 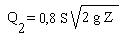, где S - площадь отверстия диаметром d=0,5 м, g= 9,81 м/с2 , Z(t) - глубина воды в резервуаре, удовлетворяющая уравнению:
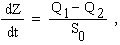
причем S0 - площадь свободной поверхности жидкости.
Необходимо при начальном условии Z=20 м при t=0 определить, через какое время t уровень жидкости перестанет понижаться.
ЗАДАЧА О РАСПРОСТРАНЕНИИ НОВОСТЕЙ
В городе живет N= 6 млн. жителей. В 8 часов утра 1/100 часть жителей города узнала по радио столичную новость, после чего радиопередатчик вышел из строя. В дальнейшем эта новость распространялась посредством общения людей друг с другом. Число жителей x(t), узнавших новость к моменту времени t, определяется уравнением:
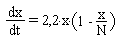
Сколько людей будет знать новость к 14 часам этого дня ?
ЗАДАЧА О БОЕВЫХ ДЕЙСТВИЯХ
Одна из противоборствующих армий x и y обладает численным преимуществом, другая - более совершенным оружием. Численный состав армий в момент времени t определяется уравнениями:
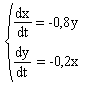
и перед началом сражения составлял x = 50 тыс. чел. у = 30 тыс. чел.
Сражение ведется до полного уничтожения одной из сторон.
Сколько будет продолжаться битва (время измеряется в сутках)?
KРИМИНАЛЬНАЯ ЗАДАЧА
При обнаружении трупа его температура составляла х=31 градус. Считая, что в момент убийства температура тела составляла х=36,6 градусов, а зависимость температуры х от времени t определяется уравнением:
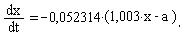
где а - температура наружного воздуха, необходимо определить, сколько времени прошло с момента убийства, если а= 23 градуса. (Время измеряется в минутах.)
ЗАДАЧА О РАСПРОСТРАНЕНИИ СЛУХОВ
В городе живет N= 5 млн. жителей. 10 ноября один из них стал распростронять слух о "важном событии". В дальнейшем эта "информация" распространялась посредством общения людей друг с другом. Число жителей x, узнавших новость к моменту времени t, определяется уравнением:
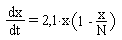
Сколько человек будут знать новость к 16 ноября ?
КРИМИНАЛЬНАЯ ЗАДАЧА
Если при обнаружении трупа измерить его температуру, то предполагая, что в момент убийства температура тела составляла 37 градусов, можно определить время, прошедшее с момента убийства, при условии, что труп не остыл до температуры окружающего воздуха. Температура тела определяется уравнением:
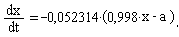
где а - температура окружающего воздуха. Пусть а=23 градуса. Необходимо определить, сколько времени прошло с момента убийства, если при обнаружении тела его температура составляла 29 градусов. (Время измеряется в минутах.)
ЗАДАЧА О ТЛЕ
Число особей x(t) в популяции яблоневой тли в момент времени t определяется уравнением:
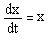
10 августа, когда начались наблюдения, было х=1000. Сколько особей было 5 августа?
ЗАДАЧА О ВОДОПРИНИМАЮЩЕМ КОЛОДЦЕ
Квадраты глубин кривой депрессии для круглого колодца удовлетворяют уравнению:
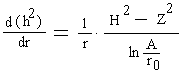
где r0=5м, Н=4м, z=8м, А=1000, а=1м (см.обозначения на рисунке).
Необходимо определить заглубление отметки поверхности грунтовых вод под поверхностью земли на расстоянии r=200 м от оси колодца (ЕУГВ - Естественный Уровень Урунтовых Вод).
ЗАДАЧА ОБ ИСТЕЧЕНИИ ЖИДКОСТИ ИЗ СФЕРИЧЕСКОГО РЕЗЕРВУАРА
Расходом Q (куб.м/сек) называется объем воды, проходящий через отверстие или трубу в единицу времени.
В сферический резервуар диаметром D=8 м поступает расход Q1=4,1 куб.м./сек. и через отверстие уходит расход , где S - площадь отверстия диаметром d=1 м, g= 9,81 м/с2 , Z(t) - глубина воды в резервуаре, удовлетворяющая уравнению:
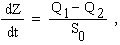
причем S0 - площадь свободной поверхности жидкости.
Необходимо при начальном условии Z=7 м при t=0 определить, через какой промежуток времени уровень воды перестанет понижаться..
ЗАДАЧА О ПОЛЕТЕ МЕТЕОРОЛОГИЧЕСКОЙ РАКЕТЫ
Запас топлива в ракете для метеоролгических измерений в верхних слоях тропосферы рассчитан на 30 сек. работы двигателя. Масса ракеты во время полета меняется по закону m(t)=M-qt , где M = 2000 кг -стартовая масса полностью заправленной топливом ракеты, q = 50 кг/сек -расход топлива, t -время, прошедшее с момента старта. Высота подъема ракеты определяется уравнением:
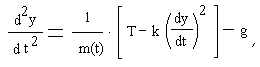
где Т = 100000кН - тяговое усилие двигателя, k = 0,3 - коэффициент, учитывающий сопротивление воздуха, g = 9,81 м/с2 - ускорение свободного падения.
К какому моменту времени ракета достигнет высоты 8 км?
ЗАДАЧА ПОСТРОЕНИЯ КРИВОЙ СВОБОДНОЙ ПОВЕРХНОСТИ ЖИДКОСТИ
Длинный канал прямоугольного поперечного сечения шириной l = 10 м, продольным уклоном дна i = 0,005 перегорожен щитом, приподнятым над дном на высоту 0,5 м.
Глубина воды в канале определяется уравнением:
,
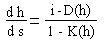где 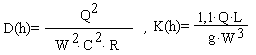, причем s -ось, направленная в сторону движения жидкости, Q = 20 куб.м./сек -расход воды, идущей по каналу, -площадь поперечного сечения потока, g = 9,81 м/с2 -ускорение свободного падения, 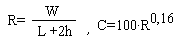-гидравлические коэффициенты.
На каком расстоянии от щита уровень воды достигнет 1м?
ХИМИЧЕСКАЯ ЗАДАЧА
Объем вещества x(t), образовавшегося в результате химической реакции к моменту времени t , определяется уравнением:
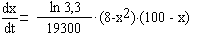
Через 20 минут после начала реакции объем вещества составлял x= 13 литров.
Необходимо определить, cколько образуется вещества через 1 час (60 минут) после начала эксперимента.
ЗАДАЧА О ПАДЕНИИ ГРУЗА
С вертолета, находящегося на высоте Н над землей сбрасывают груз массой m = 250 кг. Движение груза описывается уравнением:
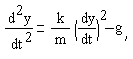
где k=0,3 - коэффициент, учитывающий сопротивление воздуха, g = 9,81 м/с2 - ускорение свободного падения, у(t) - высота груза над поверхностью земли в момент времени t. Необходимо определить время падения груза, если H = 2000м.
ЗАДАЧА ОБ ИЗГИБЕ КОНСОЛЬНОЙ БАЛКИ
Консольная балка длиной 3 м подвержена действию сосредоточенной силы величиной Р=20кН, приложенной на ее конце. Необходимо построить изогнутую ось балки и найти ее максимальный прогиб, если дифференциальное уравнение, описывающее изгиб балки, выглядит следующим образом:
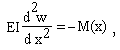
где M(x) - закон изменения изгибающего момента, Е=210 000 000 кН/кв.м. - модуль упругости стали, I=0,00001520 м4 (швеллер N 20) -момент инерции поперечного сечения балки.
ЗАДАЧА ОБ ОСАДЕ ГОРОДА
Численный состав армии, осаждающей город x(t) и обороняющей город y(t)определяется системой уравнений:
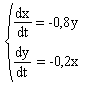
В начале осады было x = 50 тыс. чел. у = 30 тыс.чел. Осада продолжается до полного уничтожения одной из сторон.
Кто выйдет победителем, осаждающие или обороняющиеся?
ЗАДАЧА ОБ ИЗГИБЕ КОНСОЛЬНОЙ БАЛКИ
Консольная балка длиной 3 м подвержена действию сосредоточенного момента величиной М=80 КНм, приложенного на ее конце.Необходимо построить изогнутую ось балки и найти ее максимальный прогиб, если дифференциальное уравнение, описывающее изгиб балки, выглядит следующим образом:
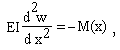
где M(x) - закон изменения изгибающего момента, Е=210 000 000 кН/кв.м. - модуль упругости стали, I=0,00001520 м4 (швеллер N 20) -момент инерции поперечного сечения балки.
ЗАДАЧА О ВОДООТДАЮЩЕМ КОЛОДЦЕ
Квадраты глубин кривой депрессии для круглого колодца удовлетворяют уравнению:
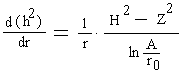
где r0=5м, Н=8м, z=4м, А=800, а=1м (см.обозначения на рисунке).
Необходимо определить заглубление отметки поверхности грунтовых вод под поверхностью земли на расстоянии r=200 м от оси колодца.
Желаем Вам приятной работы и хороших файлов !
| Вариант: |
|
ЧАСТЬ3: ЧИСЛЕННОЕ РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Задание 1. Численное решение краевой задачи с главными граничными условиями методом конечных разностей
Необходимо найти максимальный прогиб балки, изображенной на рисунке:
.
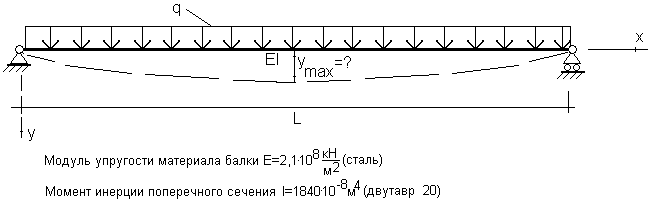
Дифференциальное уравнение изгиба балки имеет вид:
,
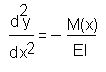где M(x) -выражение для изгибающего момента.
1. Численное решение задачи найти методом конечных разностей на сетках из 4,8,16 и 32 участков.
2. Построить графики полученных решений (ось прогибов направить вниз).
3. Найти точное решение задачи по формуле:
.
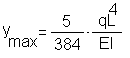4. Найти абсолютные и относительные погрешности численных решений (для максимального прогиба балки), оценить порядок сходимости метода. Результаты удобно оформить в виде таблицы:
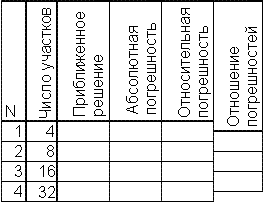
5. Сделать выводы о точности численных решений.
Задание 2. Численное решение краевой задачи с главным и естественным граничными условиями методом конечных разностей
Необходимо найти горизонтальное перемещения свободного конца стержня, изображенного на рисунке:
,
Дифференциальное уравнение продольной деформации стержня имеет вид:
,
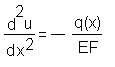где u - горизонтальные перемещения точек стержня, q(x) -интенсивность продольной распределенной нагрузки, EF- продольная жесткость стержня.
Естественное граничное условие на свободном конце стержня имеет вид:
.
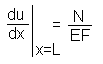1. Численное решение задачи найти методом конечных разностей на сетках из 4,8,16 и 32 участков.
2. Построить графики полученных решений u(x).
3. Найти аналитическое решение задачи.
4. Найти абсолютные и относительные погрешности численных решений (для перемещения на свободном конце стержня), оценить порядок сходимости метода. Результаты удобно оформить в виде таблицы:
5. Сделать выводы о точности численных решений.
Задание 3. Метод Ритца.
В толще высокой бетонной стенки толщиной L=2м в результате экзотермической реакции в свежеуложенном бетоне происходит повышение температуры.
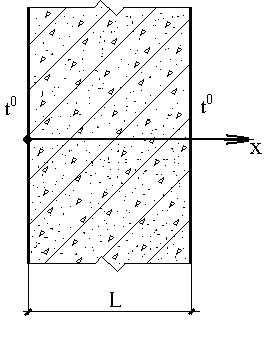
Распределение температуры по ширине стенки описывается дифференциальным уравнением и граничными условиями:
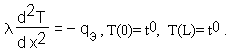
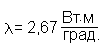- коэффициент теплопроводности бетона,
- интенсивность выделения тепла,
- температура наружного воздуха.
Эквивалентная вариационная постановка задачи формулируется следующим образом:
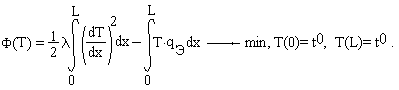
1. Методом Ритца с использованием алгебраических, тригонометрических и конечно-элементных базисных функций при n=2,3,4 , где n -номер последнего учитываемого члена суммы Ритца, найти максимальную температуру в стенке.
2. Построить графики полученных решений.
3. Найти точное решение задачи по формуле:
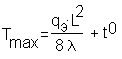
и сопоставить его с приближенными решениями.
4. Сделать выводы о точности решений, полученных методом Ритца.
Задание 4. Метод конечных элементов (МКЭ).
1. Найти решение задачи из предыдущего пункта методом конечных элементов на сетке из четырех участков: построить матрицы жесткости конечных элементов, сформировать вектор свободных членов, сформировать и решить систему разрешающих уравнений МКЭ.
2. Построить графики полученных решений.
3. Сопоставить полученное решение с точным.
Задание 5. Метод Галёркина.
Дана краевая задача:
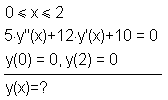
1. Найти решение задачи методом Галёркина с использованием алгебраических, тригонометрических и конечно-элементных базисных функций при n=2 и n=3, где n-количество удерживаемых в сумме Ритца членов.
2. Построить графики полученных решений.
3. Найти решение этой же задачи методом конечных разностей.
4. Сопоставить решения, полученные методом Галёркина и МКР.
Задание 6. Практическая задача.
ЧАСТЬ2: ЗАДАЧА ОТ ПОЛЕТЕ ПУЛИ
Расстояние, преодоленное пулей, выпущенной горизонтально, определяется уравнением:
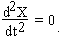
Через T0 = 2 сек. после выстрела скорость пули составляла 100 м/сек.
Найти расстояние, преодоленное пулей за 2 секунды.
Вариационная постановка задачи:
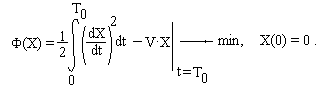
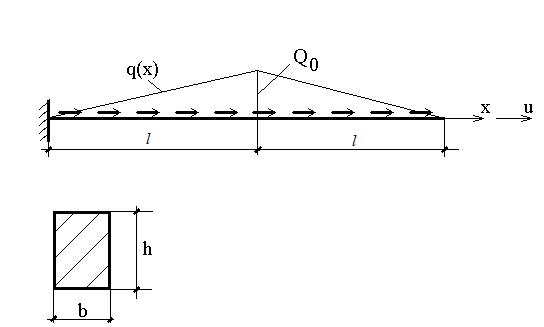
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
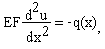
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
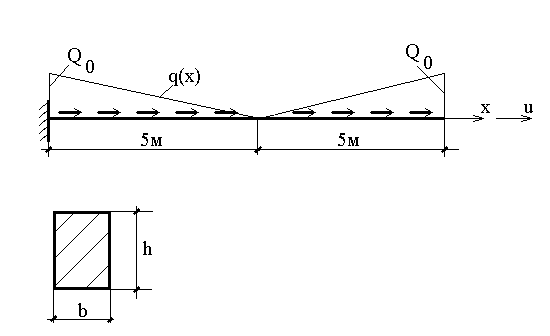
Необходимо найти функцию u(x), если h= 0,9 м , b=0,30 м , Q0=45 КН/м;
Bариационная постановка задачи:
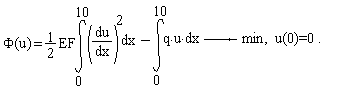
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
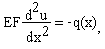
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
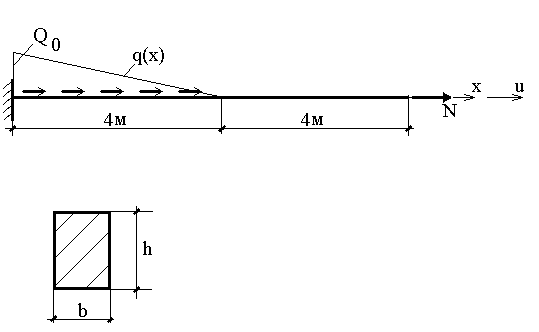
Необходимо найти функцию u(x), если h= 0,6 м , b=0,40 м , Q0=100 кН/м, N=200 кН;
Bариационная постановка задачи:
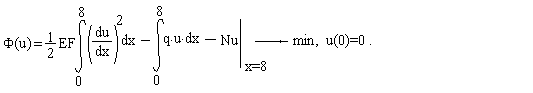
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
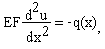
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
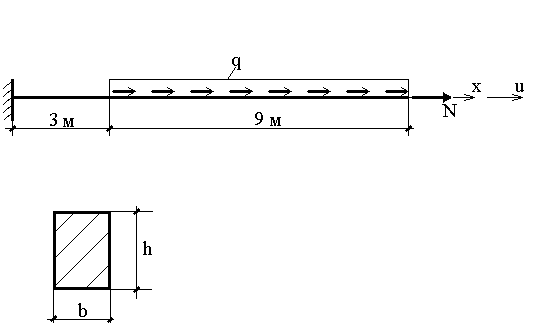
Необходимо найти функцию u(x), если h= 1,0 м , b=0,50 м , Q0=30 кН/м, N=20 кН;
Bариационная постановка задачи:
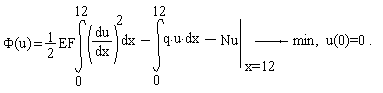
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
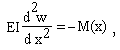
где Е=200 000 000 КН/кв.м. - модуль упругости материала балки, I - момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема стержня приведена на рисунке.
Необходимо найти функцию w(x), если I=0,00001290 м4 (двутавр N 18);
Вариационная постановка задачи:
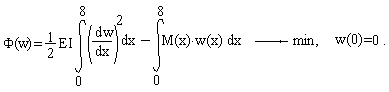
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
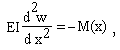
где Е=2 000 000 КН/кв.м. - модуль упругости материала балки,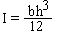 
- момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема балки и ее поперечное сечение приведены на рисунке.
Необходимо найти прогиб в центре пролета балки, если b= 0,5 м и h = 1 м;
Вариационная постановка задачи:
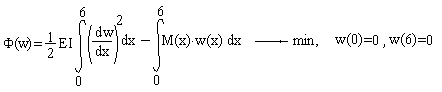
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
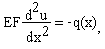
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
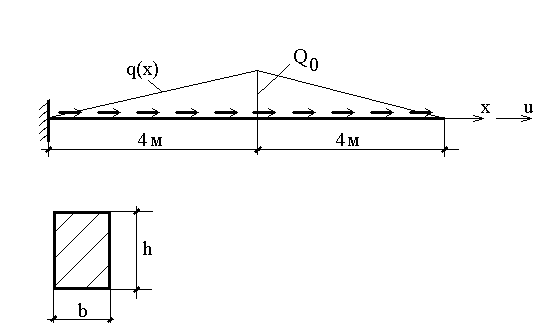
Необходимо найти функцию u(x), если h= 0,7 м , b=0,4 м , Q0=50 кН/м;
Bариационная постановка задачи:
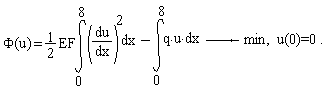
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
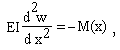
где Е=20 000 000 КН/кв.м. - модуль упругости материала балки,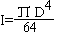 
- момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема балки и ее поперечное сечение приведены на рисунке.
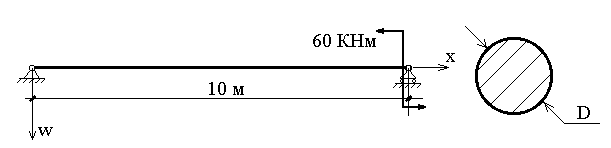
Необходимо найти прогиб в центре пролета балки, если D= 0,7 м;
Вариационная постановка задачи:
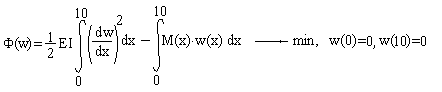
ЗАДАЧА О ПОЛЕТЕ ЯДРА
Высота вертикального подъема ядра, выпущенного из пушки, определяется уравнением:
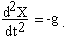
где g = 9,81 м/с2 - ускорение свободного падения.
Необходимо найти высоту максимального подъема ядра, если для ее достижения потребовалось T0=6 секунд.
Вариационная постановка задачи:
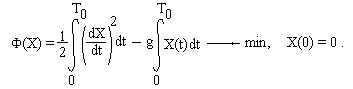
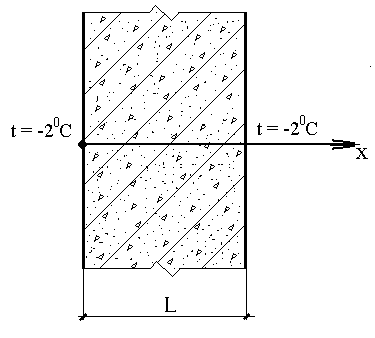
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
Распределение температуры в высокой бетонной стенке толщиной L описывается уравнением:
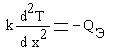
где k = 2,67 Вт/м.град. - коэффициент теплопроводности бетона, Qэ - интенсивность выделения тепла в результате экзотермической реакции в свежеуложенном бетоне. Необходимо найти распределение температуры в стенке T(x), если температура наружного воздуха составляет -2°С, толщина стенки L = 2,0 м , Qэ = 100 Вт/куб.м ;
Вариационная постановка задачи:
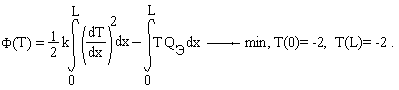
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
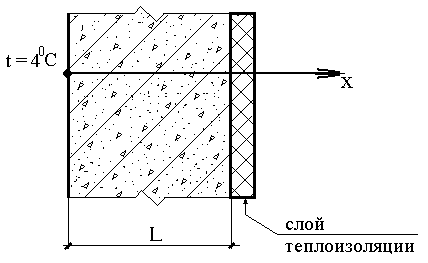
Распределение температуры в высокой бетонной стенке толщиной L описывается уравнением:
,
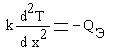где k = 2,67 Вт/м.град. - коэффициент теплопроводности бетона, Qэ - интенсивность выделения тепла в результате экзотермической реакции в свежеуложенном бетоне, L=0,8 м, Qэ=150 Вт/куб.м.. Необходимо найти распределение температуры в стенке T(x), если на одной ее стороне она равна температуре наружного воздуха t= +4°С, а другая ее сторона теплоизолирована, т.е. на ней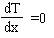 
.
Вариационная постановка задачи:
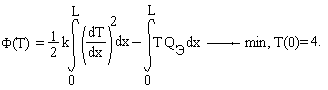
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
Полый шар, изображенный на рисунке, помещен в жидкость с температурой Т = 90°С.
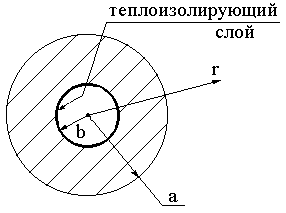
Изменение температуры вдоль радиуса r определяется уравнением:
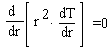
Внутренняя поверхность шара теплоизолирована, т.е. на ней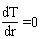 
.
Необходимо найти закон изменения температуры внутри тела T(r), если b = 2,0 м , a = 2,5 м .
Вариационная постановка задачи:
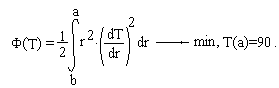
ЧАСТЬ 2: ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
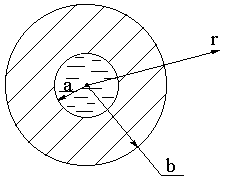
По трубе течет жидкость с температурой 80°С. Температура на внешней поверхности трубы равна 0°С. Необходимо найти распределение температуры в стенках трубы, если a = 1 м , b = 2 м, а закон распределения температуры в трубе определяется уравнением:
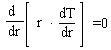
Вариационная постановка задачи:
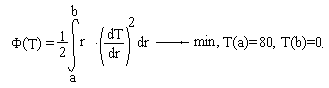
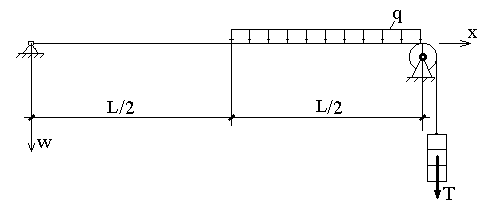
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
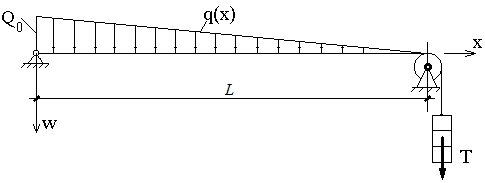
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
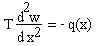
Схема нити приводится на рисунке:
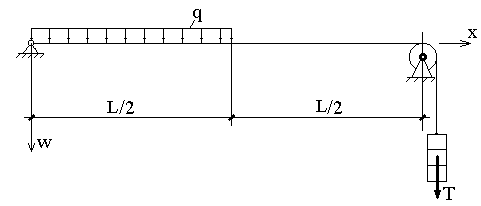
Найти прогиб нити w в точке x=L/2, если L = 10 м, q = 2 кН/м , T= 40 кН .
Вариационная постановка задачи:
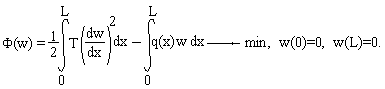
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
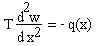
Схема нити приводится на рисунке:
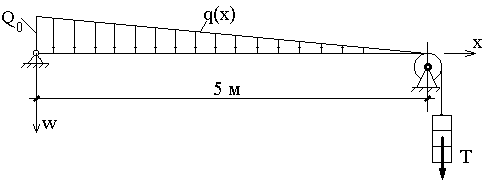
Найти максимальное значение прогиба нити w(x) и значение координаты х , при котором прогиб достигает максимального значения, если L= 5м, Q0= 15 кН/м , T= 100 кН .
Вариационная постановка задачи:
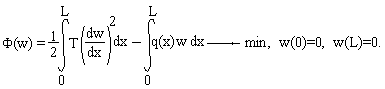
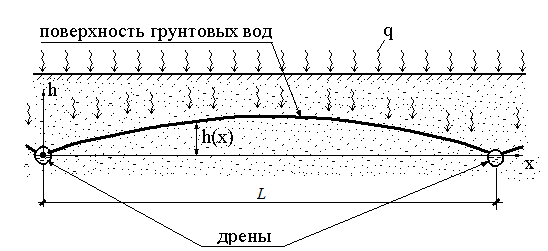
ЗАДАЧА ОБ ОТВЕДЕНИИ ГРУНТОВЫХ ВОД.
При искусственном осушении территории на расстоянии 10 метров друг от друга под поверхностью земли прокладываются дрены, отводящие грунтовую воду.
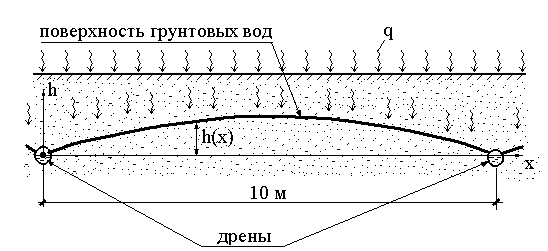
Положение поверхности грунтовых вод определяется уравнением:
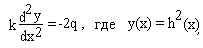
где k=0,1 м/сут (песок мелкозернистый) - коэффициент фильтрации грунта, q = 0,003 м/сут - расчетная интенсивность притока атмосферных вод с поверхности земли.
Необходимо определить, на какой глубине следует расположить дрены, если грунтовые воды не должны быть ближе к поверхности земли ближе чем на 0,5 м.
Вариационная постановка задачи:
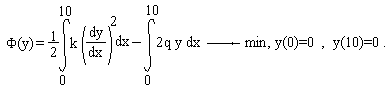
ЗАДАЧА ОБ ОТВЕДЕНИИ ГРУНТОВЫХ ВОД.
При искусственном осушении территории на расстоянии 25 метров друг от друга под поверхностью земли прорываются дренажные канавы, отводящие грунтовую воду.
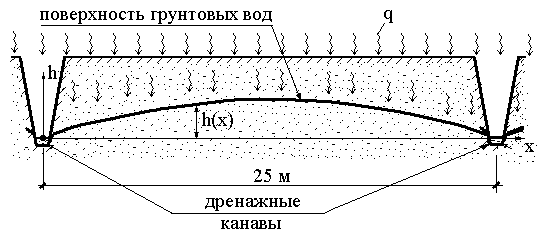
Положение поверхности грунтовых вод определяется уравнением:
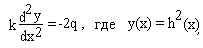
где k=1 м/сут (среднезернистый песок) - коэффициент фильтрации грунта, q = 0,001 м/сут - расчетная интенсивность притока атмосферных вод с поверхности земли.
Необходимо определить, на какой глубине следует расположить дрены, если грунтовые воды не должны быть ближе к поверхности земли ближе чем на 0,3 м.
Вариационная постановка задачи:
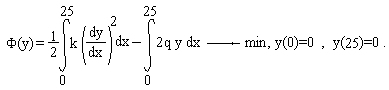
ЗАДАЧА ОБ ОТВЕДЕНИИ ГРУНТОВЫХ ВОД.
При искусственном осушении территории на расстоянии 25 метров друг от друга под поверхностью земли прорываются дренажные канавы, отводящие грунтовую воду.
Положение поверхности грунтовых вод определяется уравнением:
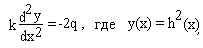
где k=1 м/сут (среднезернистый песок) - коэффициент фильтрации грунта, q = 0,0015 м/сут - расчетная интенсивность притока атмосферных вод с поверхности земли.
Необходимо определить, на какой глубине следует расположить дрены, если грунтовые воды не должны быть ближе к поверхности земли ближе чем на 0,3 м.
Вариационная постановка задачи:
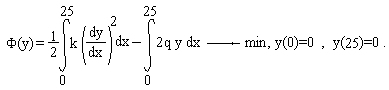
ЗАДАЧА ОБ ОТВЕДЕНИИ ГРУНТОВЫХ ВОД.
При искусственном осушении территории на расстоянии 10 метров друг от друга под поверхностью земли прокладываются дрены, отводящие грунтовую воду.
Положение поверхности грунтовых вод определяется уравнением:
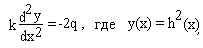
где k=0,01 м/сут (суглинок) - коэффициент фильтрации грунта, q = 0,003 м/сут - расчетная интенсивность притока атмосферных вод с поверхности земли.
Необходимо определить, на какой глубине следует расположить дрены, если грунтовые воды не должны быть ближе к поверхности земли ближе чем на 0,5 м.
Вариационная постановка задачи:
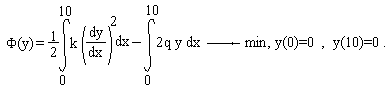
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
По трубе течет жидкость с температурой 80°С. Температура на внешней поверхности трубы равна 0°С. Необходимо найти распределение температуры в стенках трубы, если a = 2 м , b = 3 м, а закон распределения температуры в трубе определяется уравнением:
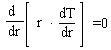
Вариационная постановка задачи:
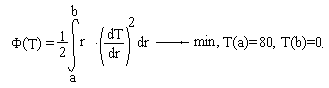
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
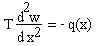
Схема нити приводится на рисунке:
Найти прогиб нити w(x) в точке x=2,5 м , если L= 5м, Q0= 20 кН/м , T= 200 кН .
Вариационная постановка задачи:
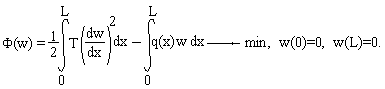
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
Полый шар, изображенный на рисунке, помещен в жидкость с температурой Т = 90°С.
Изменение температуры вдоль радиуса r определяется уравнением:
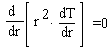
Внутренняя поверхность шара теплоизолирована, т.е. на ней .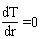
Необходимо найти закон изменения температуры внутри тела T(r), если b = 3,0 м , a = 4,0 м .
Вариационная постановка задачи:
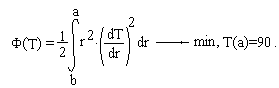
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
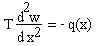
Схема нити приводится на рисунке:
Найти максимальное значение прогиба нити w и значение координаты х , при котором прогиб достигает максимального значения, если L = 6 м, q = 15 кН/м , T= 200 кН .
Вариационная постановка задачи:
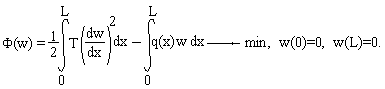
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
Распределение температуры в высокой бетонной стенке толщиной L описывается уравнением:
,
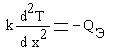где k = 2,67 Вт/м.град. - коэффициент теплопроводности бетона, Qэ - интенсивность выделения тепла в результате экзотермической реакции в свежеуложенном бетоне, L=1,0 м, Qэ=100 Вт/куб.м.. Необходимо найти распределение температуры в стенке T(x), если на одной ее стороне она равна температуре наружного воздуха t= +4°С, а другая ее сторона теплоизолирована, т.е. на ней .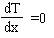
Вариационная постановка задачи:
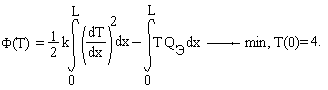
ЗАДАЧА О ПОЛЕТЕ ЯДРА
Высота вертикального подъема ядра, выпущенного из пушки, определяется уравнением:
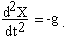
где g = 9,81 м/с2 - ускорение свободного падения.
Необходимо найти высоту максимального подъема ядра, если для ее достижения потребовалось T0=7,5 секунд.
Вариационная постановка задачи:
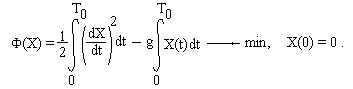
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
Распределение температуры в высокой бетонной стенке толщиной L описывается уравнением:
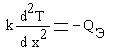
где k = 2,67 Вт/м град - коэффициент теплопроводности бетона, Qэ - интенсивность выделения тепла в результате экзотермической реакции в свежеуложенном бетоне. Необходимо найти распределение температуры в стенке T(x), если температура наружного воздуха составляет -2°С, толщина стенки L = 1,5 м , Qэ = 150 Вт/куб.м ;
Вариационная постановка задачи:
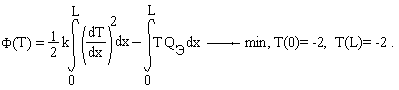
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
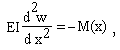
где Е=20 000 000 КН/кв.м. - модуль упругости материала балки, 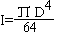- момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема балки и ее поперечное сечение приведены на рисунке.
Необходимо определить, на каком расстоянии х от левой опоры прогиб достигает максимального значения и какова его величина в этой точке, если D = 0,8 м .
Вариационная постановка задачи:
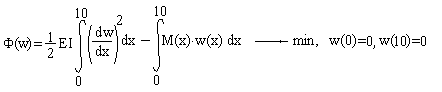
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
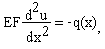
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
Необходимо найти функцию u(x), если h= 0,5 м , b=0,3 м , Q0=40 кН/м;
Bариационная постановка задачи:
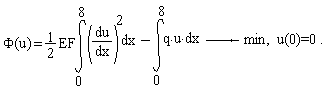
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
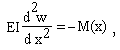
где Е=2 000 000 КН/кв.м. - модуль упругости материала балки, 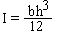- момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема балки и ее поперечное сечение приведены на рисунке.
Необходимо определить координату точки, в которой прогиб балки достигает максимального значения, и величину этого прогиба, если b= 0,4 м и h = 1 м;
Вариационная постановка задачи:
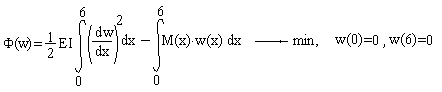
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
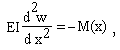
где Е=200 000 000 КН/кв.м. - модуль упругости материала балки, I - момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема стержня приведена на рисунке.
Необходимо найти функцию w(x), если I=0,00001520 м4 (швеллер N 20);
Вариационная постановка задачи:
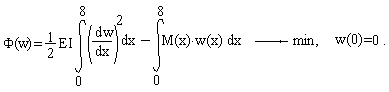
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
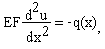
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
Необходимо найти функцию u(x), если h= 0,8 м , b=0,60 м , Q0=10 кН/м, N=100 кН;
Bариационная постановка задачи:
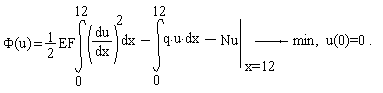
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
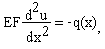
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
Необходимо найти функцию u(x), если h= 0,50 м , b=0,40 м , Q0=110 кН/м, N=100 кН;
Bариационная постановка задачи:
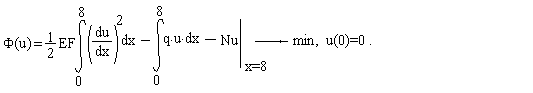
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
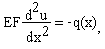
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
Необходимо найти функцию u(x), если h= 1,0 м , b=0,35 м , Q0=50 КН/м;
Bариационная постановка задачи:
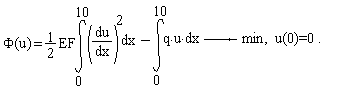
ЗАДАЧА ОТ ПОЛЕТЕ ПУЛИ
Расстояние, преодоленное пулей, выпущенной горизонтально, определяется уравнением:
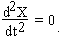
Через T0 = 3 сек. после выстрела скорость пули составляла 120 м/сек.
Найти расстояние, преодоленное пулей за 3 секунды.
Вариационная постановка задачи:
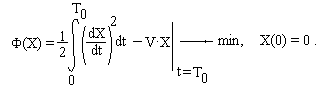
| Вариант: |
|
ЧАСТЬ4: МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ. ОСНОВЫ МКЭ
Задание.
1. Найти точное решение задачи, решив дифференциальное уравнение.
2.1 Найти решение задачи, используя метод Ритца. Координатные функции в сумме Ритца выбрать самостоятельно. Рассмотреть два варианта слагаемых (N и N+1) в сумме Ритца(N -- минимальное число слагаемых, подходящих для решения вариационной задачи)
2.2 Построить графики найденных методом Ритца функций. Выбрать наиболее точную.
3.1 Найти решение задачи методом конечных элементов на трех сетках (1КЭ, 2КЭ, 4КЭ или 2КЭ, 4КЭ, 8КЭ) с использованием полиномов Лагранжа.
3.2 Построить графики найденных МКЭ функций с использованием полиномов Лагранжа. Выбрать наиболее точную.
4.1 Найти решение задачи методом конечных элементов на трех сетках (1КЭ, 2КЭ, 4КЭ или 2КЭ, 4КЭ, 8КЭ) с использованием кусочно-линейных функций: построить матрицы жесткости конечных элементов, сформировать вектор свободных членов и глобальную матрицу жесткости всей системы, учесть граничные условия, сформировать и решить систему разрешающих уравнений МКЭ.
4.2 Построить графики найденных МКЭ функций. Выбрать наиболее точную
5. Построить графики четырех решений (Точное решение, более точное решение по методу Ритца, более точное решение по МКЭ: полиномы Лагранжа, более точное решение по МКЭ: кусочно-линейные функции).
6. Оценить погрешность для всех приблеженных решений по сравнению с точным.
7. Оценить погрешность для МКЭ решения используя метод Шварцмана
ЗАДАЧА ОТ ПОЛЕТЕ ПУЛИ
Расстояние, преодоленное пулей, выпущенной горизонтально, определяется уравнением:
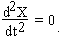
Через T0 после выстрела скорость пули составляла V0.
Найти функцию x(t) и расстояние, преодоленное пулей за T0 секунды.
Вариационная постановка задачи:
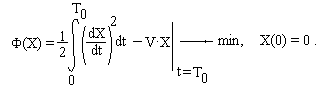
| Вариант 1 | Вариант 2 | Вариант 3 | |
| T0 | 2 c | 3,5 c | 1,8 c |
| V0 | 100 м/c | 175 м/с | 130 м/с |
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
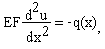
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
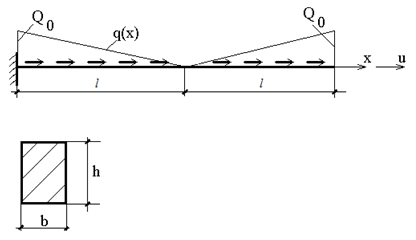
Необходимо найти функцию u(x), если h= 0,9 м , b=0,30 м;
Bариационная постановка задачи:
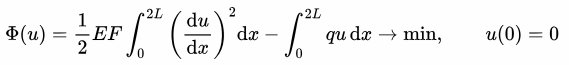
| Вариант 1 | Вариант 2 | Вариант 3 | |
| Q0 | 28 КН/м | 45 КН/м | 60 КН/м |
| l | 5м | 7м | 6м |
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
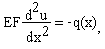
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
Необходимо найти функцию u(x), если известны h, b, Q0, N, l;
Bариационная постановка задачи:
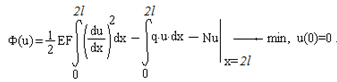
| Вариант 1 | Вариант 2 | Вариант 3 | |
| h | 0,6 м | 0,8 м | 0,7 м |
| b | 0.35 м | 0.45 м | 0.50 м |
| Q0 | 100 КН/м | 125 КН/м | 150 КН/м |
| N | 200 кН | 160 кН | 180 кН |
| l | 4 м | 5 м | 6 м |
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
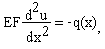
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
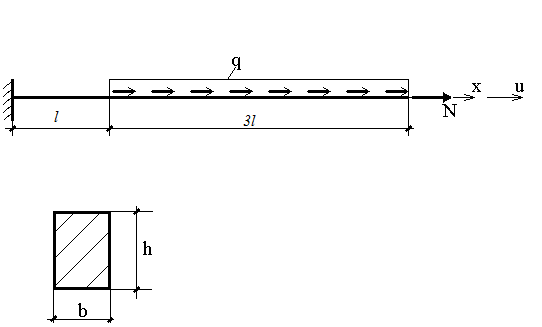
Необходимо найти функцию u(x), если h= 1,0 м , b=0,50 м , Q0=30 кН/м;
Bариационная постановка задачи:
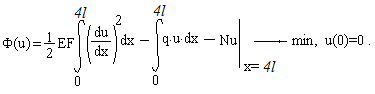
| Вариант 1 | Вариант 2 | Вариант 3 | |
| N | 20 кН | 30 кН | 45 кН |
| l | 2 м | 3 м | 2.5 м |
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
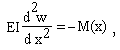
где Е=200 000 000 КН/кв.м. - модуль упругости материала балки, I - момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема стержня приведена на рисунке.
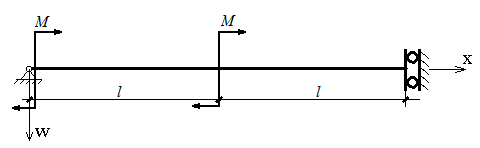
Необходимо найти функцию w(x), если I=0,00001290 м4 (двутавр N 18);
Вариационная постановка задачи:
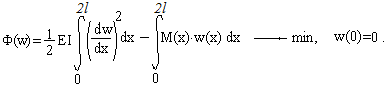
| Вариант 1 | Вариант 2 | Вариант 3 | |
| M | 22 кН/м | 37 кН/м | 44 кН/м |
| l | 4 м | 6 м | 5 м |
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
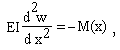
где Е=2 000 000 КН/кв.м. - модуль упругости материала балки, 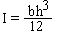- момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема балки и ее поперечное сечение приведены на рисунке.
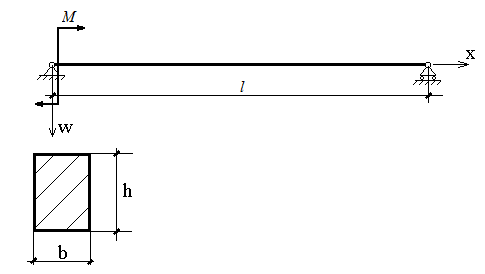
Необходимо найти прогиб в центре пролета балки, если b= 0,5 м и h = 1 м;
Вариационная постановка задачи:
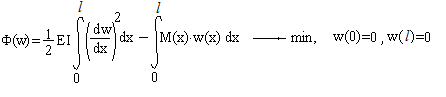
| Вариант 1 | Вариант 2 | Вариант 3 | |
| M | 75 кН | 82 кН | 94 кН |
| l | 6 м | 7,2 м | 8,1 м |
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
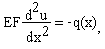
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
Необходимо найти функцию u(x), если h= 0,7 м , b=0,4 м>;
Bариационная постановка задачи:
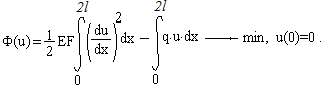
| Вариант 1 | Вариант 2 | Вариант 3 | |
| Q0 | 57 кН | 63 кН | 41 кН |
| l | 4,1 м | 5,3 м | 6,9 м |
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
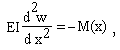
где Е=20 000 000 КН/кв.м. - модуль упругости материала балки, 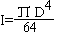- момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема балки и ее поперечное сечение приведены на рисунке.
Необходимо найти прогиб в центре пролета балки, если известны D, l, M;
Вариационная постановка задачи:
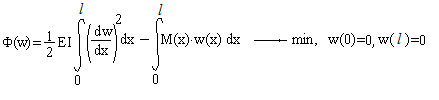
| Вариант 1 | Вариант 2 | Вариант 3 | |
| D | 0,7 м | 0,3 м | 0,5 м |
| l | 10 м | 9 м | 11 м |
| M | 62 кНм | 71 кНм | 89 кНм |
ЗАДАЧА О ПОЛЕТЕ ЯДРА
Высота вертикального подъема ядра, выпущенного из пушки, определяется уравнением:
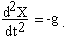
где g - ускорение свободного падения.
Необходимо найти высоту максимального подъема ядра, если для ее достижения потребовалось T0 секунд.
Вариационная постановка задачи:
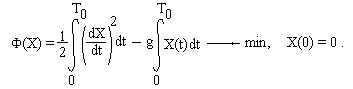
| Вариант 1 | Вариант 2 | Вариант 3 | |
| T0 | 6 с | 8 с | 10 с |
| g | 9,81 м/с2 (Земля) | 1,62 м/с2 (Луна) | 23,95 м/с2 (Юпитер) |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
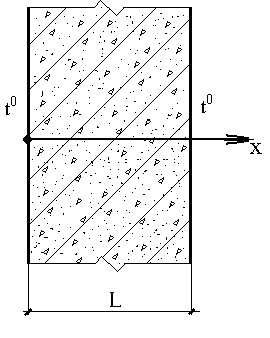
Распределение температуры в высокой бетонной стенке толщиной L описывается уравнением:
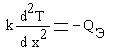
где k = 2,67 Вт/м.град. - коэффициент теплопроводности бетона, Qэ - интенсивность выделения тепла в результате экзотермической реакции в свежеуложенном бетоне. Необходимо найти распределение температуры в стенке T(x), если известна температура наружного воздуха t0, толщина стенки L, Qэ = 100 Вт/куб.м ;
Вариационная постановка задачи:
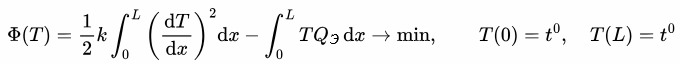
| Вариант 1 | Вариант 2 | Вариант 3 | |
| t0 | -5°С | -12°С | +2°С |
| L | 2 м | 3 м | 4 м |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
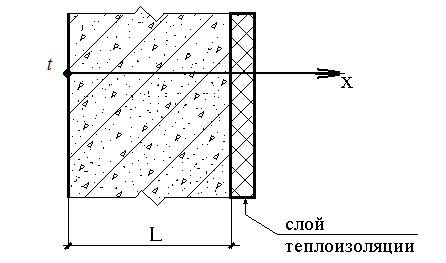
Распределение температуры в высокой бетонной стенке толщиной L описывается уравнением:
,
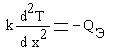где k = 2,67 Вт/м.град. - коэффициент теплопроводности бетона, Qэ - интенсивность выделения тепла в результате экзотермической реакции в свежеуложенном бетоне, Qэ=150 Вт/куб.м. Необходимо найти распределение температуры в стенке T(x), если на одной ее стороне она равна температуре наружного воздуха t, а другая ее сторона теплоизолирована, т.е. на ней .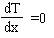
Вариационная постановка задачи:
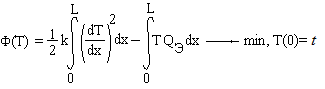
| Вариант 1 | Вариант 2 | Вариант 3 | |
| t | +4°С | -10°С | -5°С |
| L | 1 м | 1,9 м | 1,5 м |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
Полый шар, изображенный на рисунке, помещен в жидкость с температурой Т.
Изменение температуры вдоль радиуса r определяется уравнением:
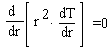
Внутренняя поверхность шара теплоизолирована, т.е. на ней .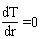
Необходимо найти закон изменения температуры внутри тела T(r), если известны b , a и Т.
Вариационная постановка задачи:
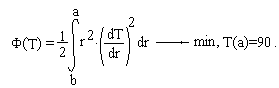
| Вариант 1 | Вариант 2 | Вариант 3 | |
| a | 2,5 м | 2,2 м | 2,9 м |
| b | 1,5 м | 1,9 м | 1,7 м |
| T | 90°С | 95°С | 105°С |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
По трубе течет жидкость с температурой T1. Температура на внешней поверхности трубы равна T2. Необходимо найти распределение температуры в стенках трубы, если a = 1 м , b = 2 м, а закон распределения температуры в трубе определяется уравнением:
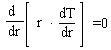
Вариационная постановка задачи:
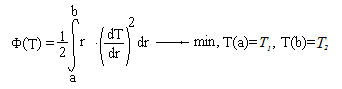
| Вариант 1 | Вариант 2 | Вариант 3 | |
| T1 | +88°С | +95°С | +109°С |
| T2 | +0°С | +9°С | +5°С |
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
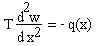
Схема нити приводится на рисунке:
Найти прогиб нити w в точке x=L/2, если известны L , q , T .
Вариационная постановка задачи:
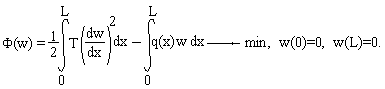
| Вариант 1 | Вариант 2 | Вариант 3 | |
| L | 10 м | 12 м | 11 м |
| q | 2,3 кН/м | 3,5 кН/м | 2,9 кН/м |
| T | 40 кН | 37 кН | 51 кН |
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
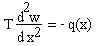
Схема нити приводится на рисунке:
Найти максимальное значение прогиба нити w(x) и значение координаты х , при котором прогиб достигает максимального значения, если известны L , Q0 , T .
Вариационная постановка задачи:
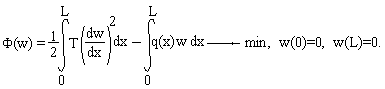
| Вариант 1 | Вариант 2 | Вариант 3 | |
| L | 5 м | 7 м | 8 м |
| Q0 | 15 кН/м | 25 кН/м | 32 кН/м |
| T | 100 кН | 121 кН | 105 кН |
ЗАДАЧА ОБ ОТВЕДЕНИИ ГРУНТОВЫХ ВОД.
При искусственном осушении территории на расстоянии L метров друг от друга под поверхностью земли прокладываются дрены, отводящие грунтовую воду.
Положение поверхности грунтовых вод определяется уравнением:
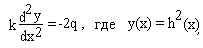
где k - коэффициент фильтрации грунта, q - расчетная интенсивность притока атмосферных вод с поверхности земли.
Необходимо определить, на какой глубине следует расположить дрены, если грунтовые воды должны быть к поверхности земли не ближе чем на a м.
Вариационная постановка задачи:
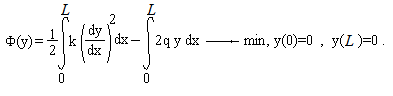
| Вариант 1 | Вариант 2 | Вариант 3 | |
| k | 0,1 м/сут (песок мелкозернистый) | 12 м/сут (песок среднезернистый) | 0,001 м/сут (суглинок) |
| q | 0,003 м/сут | 0,050 м/сут | 0,001 м/сут |
| a | 0,5 м | 0,7 м | 0,6 м |
| L | 10 м | 12 м | 15 м |
ЗАДАЧА ОБ ОТВЕДЕНИИ ГРУНТОВЫХ ВОД.
При искусственном осушении территории на расстоянии L метров друг от друга под поверхностью земли прорываются дренажные канавы, отводящие грунтовую воду.
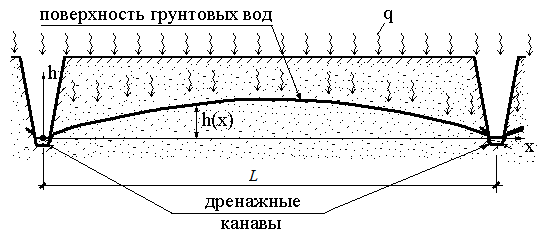
Положение поверхности грунтовых вод определяется уравнением:
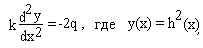
где k - коэффициент фильтрации грунта, q - расчетная интенсивность притока атмосферных вод с поверхности земли.
Необходимо определить, на какой глубине следует расположить дрены, если грунтовые воды не должны быть ближе к поверхности земли ближе чем на a м.
Вариационная постановка задачи:
| Вариант 1 | Вариант 2 | Вариант 3 | |
| k | 0,4 м/сут (песок мелкозернистый) | 6 м/сут (песок среднезернистый) | 0,003 м/сут (суглинок) |
| q | 0,003 м/сут | 0,050 м/сут | 0,001 м/сут |
| a | 0,3 м | 0,6 м | 0,8 м |
| L | 25 м | 20 м | 27 м |
ЗАДАЧА О РАСТЯЖЕНИИ СТЕРЖНЯ
Горизонтальные перемещения точек стержня u(x) определяются уравнением:
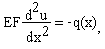
где Е=20 000 000 КН/кв.м. - модуль упругости материала стержня, F - площадь поперечного сечения, q(x) -закон изменения интенсивности растягивающей нагрузки. Схема стержня и его поперечное сечение приведены на рисунке.
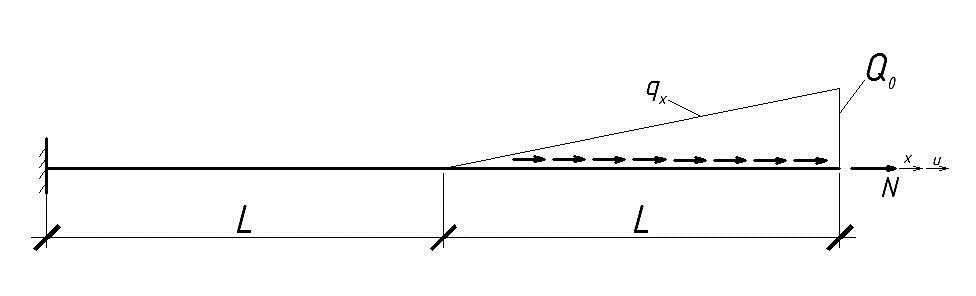
Необходимо найти функцию u(x), если h= 0,8 м , b=0,30 м и известны L , Q0, N;
Bариационная постановка задачи:
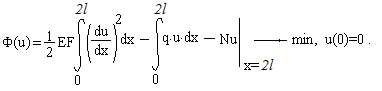
| Вариант 1 | Вариант 2 | Вариант 3 | |
| Q0 | 150 кН/м | 170 кН/м | 190 кН/м |
| N | 230 кН | 270 кН | 245 кН |
| L | 3,5 м | 4,1 м | 4,9 м |
ЗАДАЧА ОБ ИЗГИБЕ БАЛКИ
Вертикальные перемещения точек балки w(x) определяются уравнением:
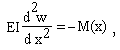
где Е=200 000 000 КН/кв.м. - модуль упругости материала балки, I - момент инерции поперечного сечения, М(x) -закон изменения изгибающего момента. Схема стержня приведена на рисунке.
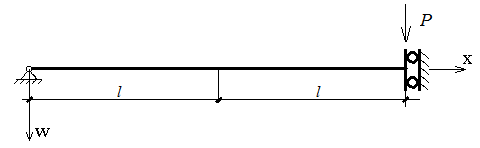
Необходимо найти функцию w(x), если известны L , h= 0,75 м , b=0,35 м , P;
Вариационная постановка задачи:
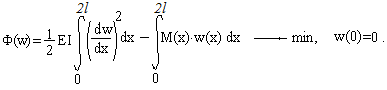
| Вариант 1 | Вариант 2 | Вариант 3 | |
| P | 120 кН | 135 кН | 155 кН |
| L | 4,5 м | 5,6 м | 3,9 м |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
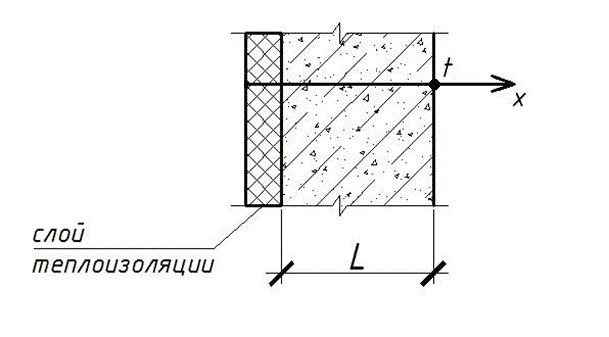
Распределение температуры в высокой бетонной стенке толщиной L описывается уравнением:
,
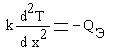где k = 2,67 Вт/м.град. - коэффициент теплопроводности бетона, Qэ - интенсивность выделения тепла в результате экзотермической реакции в свежеуложенном бетоне, Qэ=100 Вт/куб.м.. Необходимо найти распределение температуры в стенке T(x), если на одной ее стороне она равна температуре наружного воздуха t, а другая ее сторона теплоизолирована, т.е. на ней .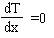
Вариационная постановка задачи:
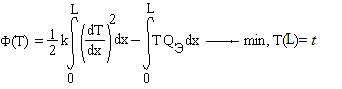
| Вариант 1 | Вариант 2 | Вариант 3 | |
| t | -2°С | -10°С | -7°С |
| L | 0,9 м | 1,7 м | 1,3 м |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
В полый шар, изображенный на рисунке, залита жидкость с температурой Т.
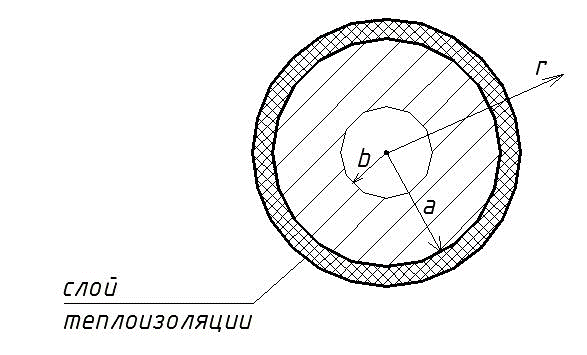
Изменение температуры вдоль радиуса r (b < r < a) определяется уравнением:
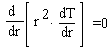
Наружняя поверхность шара теплоизолирована, т.е. на ней .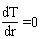
Необходимо найти закон изменения температуры внутри тела T(r), если известны b = 0,15 м , a , T.
Вариационная постановка задачи:
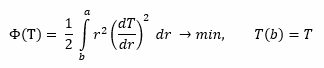
| Вариант 1 | Вариант 2 | Вариант 3 | |
| T | 110°С | 145°С | 127°С |
| a | 2,5 м | 3,0 м | 2,2 м |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
Полый шар, изображенный на рисунке, помещен в жидкость с температурой t1.
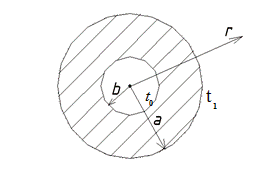
Изменение температуры вдоль радиуса r (b < r < a) определяется уравнением:
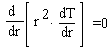
Внутрь шара залита жидкость с температурой t0.
Необходимо найти закон изменения температуры внутри тела T(r), если b = 0,5 м , a = 0,9 м .
Вариационная постановка задачи:
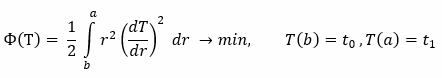
| Вариант 1 | Вариант 2 | Вариант 3 | |
| t1 | 90°С | 102°С | 97°С |
| t0 | 2°С | 7°С | -1°С |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
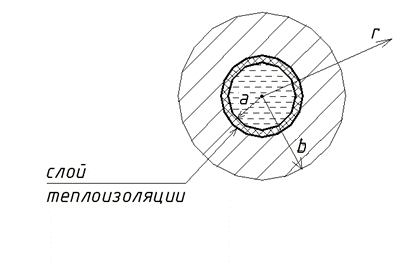
Внутренная поверхность трубы (r = a = 0.25 м) теплоизолирована, т.е. на ней .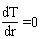
Температура на внешней поверхности трубы равна T2. Необходимо найти распределение температуры T(r) в стенках трубы (a < r < b), если известно b , а закон распределения температуры в трубе определяется уравнением:
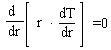
Вариационная постановка задачи:
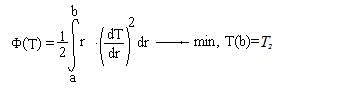
| Вариант 1 | Вариант 2 | Вариант 3 | |
| T2 | 87°С | 97°С | 103°С |
| b | 1,7 м | 2,1 м | 2,3 м |
ЗАДАЧА О РАСПРЕДЕЛЕНИИ ТЕМПЕРАТУРЫ
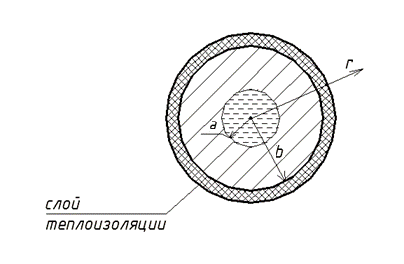
По трубе течет жидкость с температурой T1. Внешняя поверхность трубы (r = b = 1,7 м) теплоизолирована, т.е. на ней .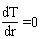
Необходимо найти распределение температуры T(r) в стенках трубы (a < r < b), если известно a, а закон распределения температуры в трубе определяется уравнением:
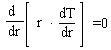
Вариационная постановка задачи:
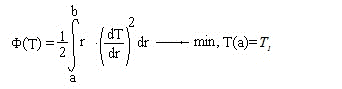
| Вариант 1 | Вариант 2 | Вариант 3 | |
| T1 | 150°С | 173°С | 161°С |
| a | 0,3 м | 0,15 м | 0,43 м |
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
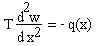
Схема нити приводится на рисунке:
Найти прогиб нити w в точке x=L/2, если известны L , q , T .
Вариационная постановка задачи:
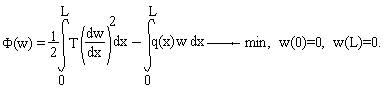
| Вариант 1 | Вариант 2 | Вариант 3 | |
| L | 14.6 м | 16.8 м | 12.2 м |
| q | 3.2 кН/м | 5.4 кН/м | 4.1 кН/м |
| T | 85 кН | 98 кН | 104 кН |
ЗАДАЧА О РАВНОВЕСИИ СТРУНЫ
Равновесие тонкой нити (струны) длиной L, натянутой с усилием Т и подверженной действию распределенной нагрузки q(x), описывается уравнением:
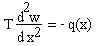
Схема нити приводится на рисунке:
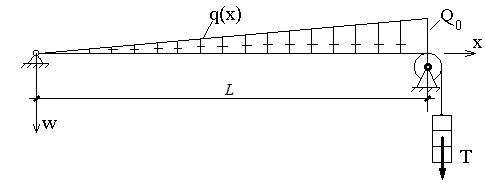
Найти максимальное значение прогиба нити w(x) и значение координаты х , при котором прогиб достигает максимального значения, если известны L, Q0 , T .
Вариационная постановка задачи:
| Вариант 1 | Вариант 2 | Вариант 3 | |
| L | 7,2 м | 8,8 м | 9,2 м |
| Q0 | 33 кН/м | 40 кН/м | 52 кН/м |
| T | 125 кН | 155 кН | 130 кН |
ЗАДАЧА О ПОСАДКЕ НА ЛУНУ
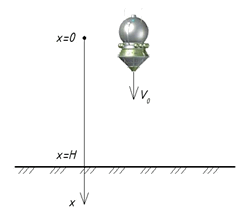
При посадке космического аппарата на Луну расстояние x(t)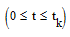 
от точки начала торможения определяется уравнением:
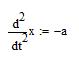
где a (м/с^2) - ускорение, создаваемое тормозящими двигателями.
Граничные условия:
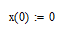
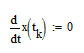- скорость в момент посадки д.б. равна нулю.
Найти функцию x(t) и ответить на вопросы:
1. Какова скорость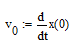 
в момент начала торможения?
2. На какой высоте H нужно начинать торможение?
Функционал вариационной постановки задачи:
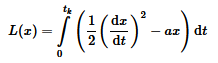
| Вариант 1 | Вариант 2 | Вариант 3 | |
| a | 0,2 м/c2 | 0,5 м/c2 | 0,35 м/c2 |
| tk | 95 c | 111 c | 56 c |
ЗАДАЧА О ПРИТЯЖЕНИИ МАССЫ К ОТРЕЗКУ
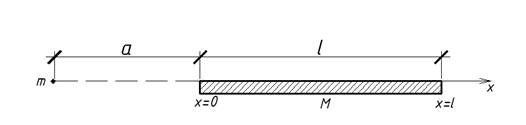
Сила F(x), с которой масса m притягивается отрезком стержня длинной l, удовлетворяет дифференциальному уравнению:
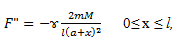
где М = 100кг -- масса стержня, l -- длина стержня, а -- расстояние от массы до левого конца стержня,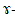 
-- гравитационная постоянная (6,67*10^11 м^3/(кг*с2)).
Граничные условия:
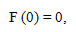
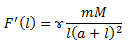
Найти F(l) -- силу притяжения массы m всем стержнем, если известны а , l.
Функционал вариационной постановки задачи:
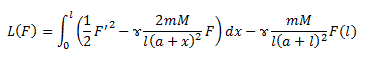
| Вариант 1 | Вариант 2 | Вариант 3 | |
| m | 2 кг | 5 кг | 7 кг |
| a | 1,2 м | 1,4 м | 0,9 м |
| l | 2,3 м | 4,1 м | 3,2 м |
ЗАДАЧА ОБ ИЗГИБНЫХ КОЛЕБАНИЙ БАЛКИ
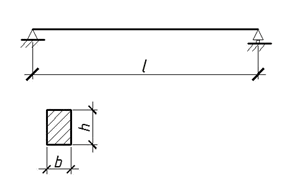
Форма колебаний шарнирно-опертой балки прямоугольного сечения (b х h) с частотой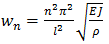 
задана функцией 
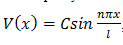, где l -- длина балки, 
(кг/м) -- погонная плотность, EI -- жетскость на изгиб. При таких колебаниях, изгибающий момент М(х) определяется дифференциальным уравнением:
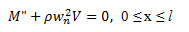
Материал балки -- сталь обыкновенная. Известны С , b = 10см, h = 30см.
Найти функцию M(x), если заданы значения n , l .
Функционал вариационной постановки задачи:
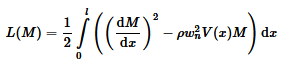
| Вариант 1 | Вариант 2 | Вариант 3 | |
| n | 3 | 5 | 7 |
| C | 0,2 м | 0,3 м | 0,4 м |
| l | 3,6 м | 4,2 м | 5,1 м |
ЗАДАЧА ОБ ИЗГИБЕ ВРАЩАЮЩЕГОСЯ ВАЛА
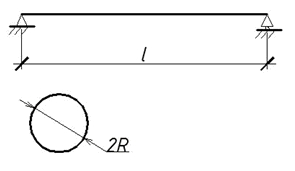
Прямой шарнирно-опертый вал длиной l круглого сечения с радиусом R вращается вокруг своей оси с угловой скоростью w. При критических значениях угловой скорости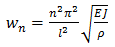 
, ((кг/м)-- погонная плотность вала, EI- жесткость на изгиб), вал принимает изогнутую форму 
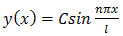(С = 0,1м). При этом изгибающий момент будет удовлетворять дифференциальному уравнению
:
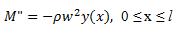
Материал балки -- сталь обыкновенная.
Найти функцию M(x), если заданы значения n ; l = 4,7м.
Функционал вариационной постановки задачи:
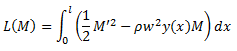
| Вариант 1 | Вариант 2 | Вариант 3 | |
| n | 2 | 4 | 8 |
| R | 2 cм | 3 cм | 4 cм |
| l | 4,7 м | 5,3 м | 6,9 м |
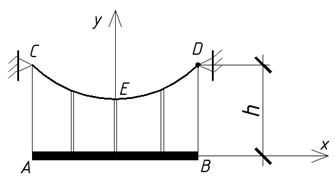
ЗАДАЧА О ПОДВЕСНОМ МОСТЕ
Мост АВ длиной 2L подвешен на тросе СЕD.
Форма троса у(х) определяется дифференциальным уравнением: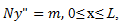 
, где N = 25кН -- горизонтальное натяжение троса в точке Е, m (кН/м) – погонный вес моста.
Граничные условия:
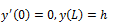
Найти максимальный "прогиб" троса (разность точек D и E), если заданы значения m ; h .
Функционал вариационной постановки задачи:
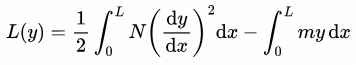
| Вариант 1 | Вариант 2 | Вариант 3 | |
| h | 6 м | 5 м | 7 м |
| m | 7 кН/м | 12 кН/м | 10 кН/м |
| L | 7 м | 8 м | 9 м |
ЗАДАЧА О ДАВЛЕНИИ ЗЕРНА В СОСУДЕ
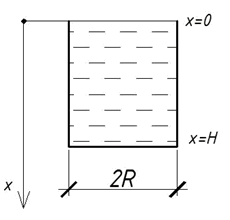
В вертикальный цилиндрический сосуд радиуса R насыпано зерно с удельным весом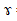 
= 7,8кН/м^3. Давление зерна р(х) на глубине х определяется дифференциальным уравнением:
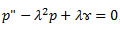
Где,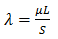 
, 
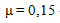-- коэффициент трения зерна о стенки сосуда, L - периметр сечения сосуда, S - площадь поперечного сечения.
Граничные условия:
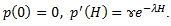
Найти функцию р(х), если заданы R и H .
Функционал вариационной постановки задачи:
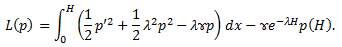
| Вариант 1 | Вариант 2 | Вариант 3 | |
| H | 6,5 м | 10,1 м | 8,4 м |
| R | 0,9 м | 1,2 м | 1,8 м |
ЗАДАЧА О ПРОХОЖДЕНИИ СВЕТА ЧЕРЕЗ СТЕКЛЯННУЮ ПЛАСТИНУ
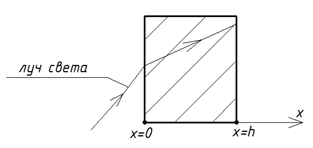
При прохождении света через плоскопараллельную стеклянную пластину толщиной h его сила J(x) (кд) определяется дифференциальным уравнением:
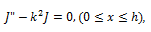
Где, где k = 0,25 м^(-1) – коэффициент поглощения.
Граничные условия:
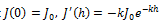
Найти силу света на выходе из пластины, если заданы J0 = 120 кд , h = 18см.
Функционал вариационной постановки задачи:
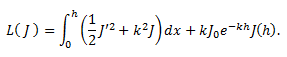
| Вариант 1 | Вариант 2 | Вариант 3 | |
| J0 | 120 кд | 150 кд | 80 кд |
| h | 18 cм | 12 cм | 21 cм |